02. Line Drawing

This is (a slightly simplified version of) how I currently draw my fully aliased (sic) lines.

The code was initially written some time after watching Casey's video discussing the issue, so I can't say how much it was influenced by it. I have a feeling there may be some similarity to Bresenham's algorithm, but I haven't looked at it yet. As in large part my current programming practice in general and this project in particular are more focused on improving my skills than quickly achieving results, I've tried to solve problems at least to a functional level myself, before possibly finding a better version from someone else.

If you don't want that opportunity spoiled for yourself I recommend you stop reading here, implement an algorithm for drawing straight lines for yourself, then come back and compare techniques.

All done? Probably not... ah well, read on anyway...

The Problem:
We would like to be able to draw a straight line from any one pixel (A) to any other (B).

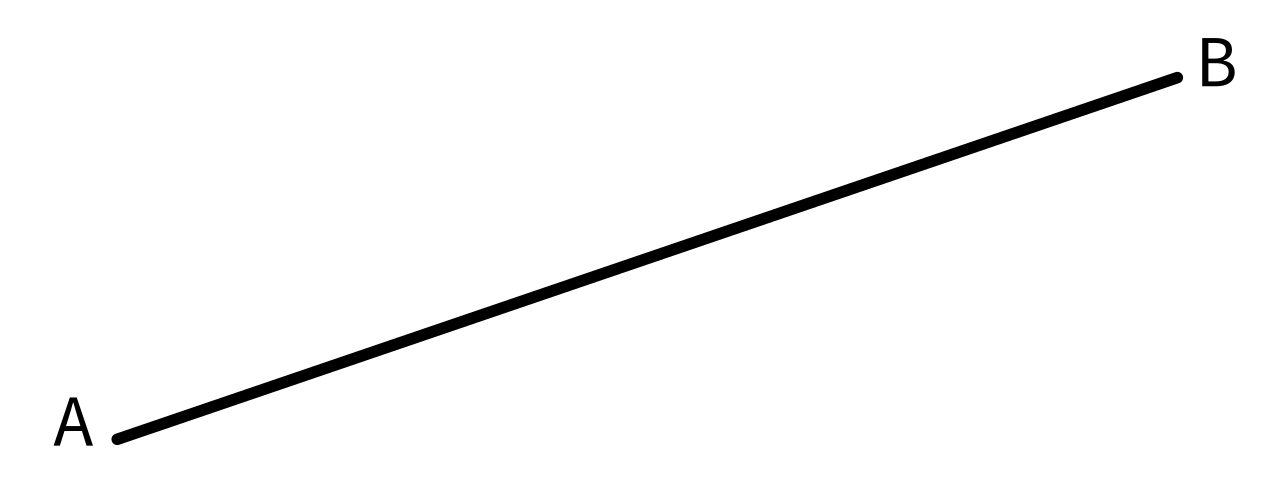
Figure 1: A straight line from A to B

The main issue here is that pixels are on a square grid with finite resolution, so from 1 pixel to the next we can only move in 3 types of directions: horizontally (a), vertically (b) and diagonally at exactly 45° (c).

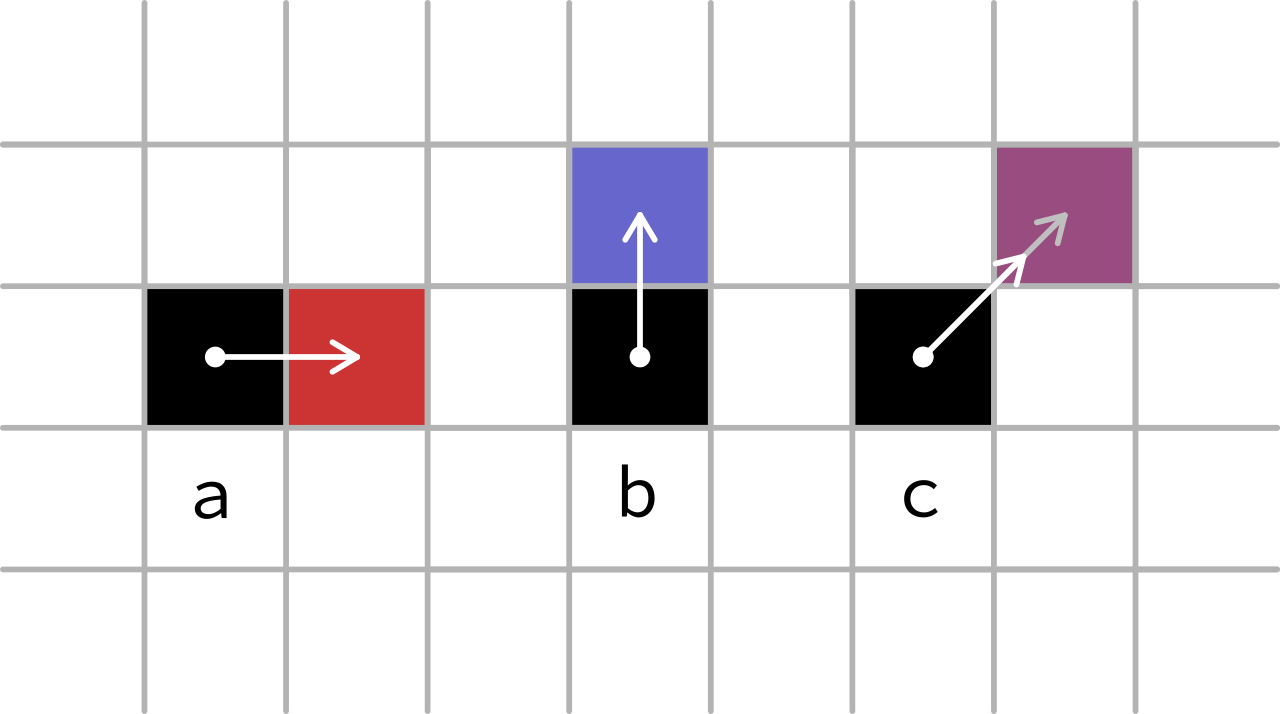
Figure 2: Pixel directions

Note that the arrow for (c) needs to be longer (all the white arrows are the same length). For the same number of pixels drawn, a 45° line will be √2 times longer than the horizontal or vertical line.

Abstract Solution:
(N.B. I am considering the location of pixels to be their centre, not their bottom-left corner... adapt as appropriate)

It's clear that we can't get a perfect line at arbitrary angles, so we'll have to approximate.

Assuming we want the line to be contiguous, after the first pixel the next will always be +/-1 horizontally, vertically or both. Ignoring horizontal, vertical and 45° lines for a moment, we can consider lines as predominantly horizontal or predominantly vertical:

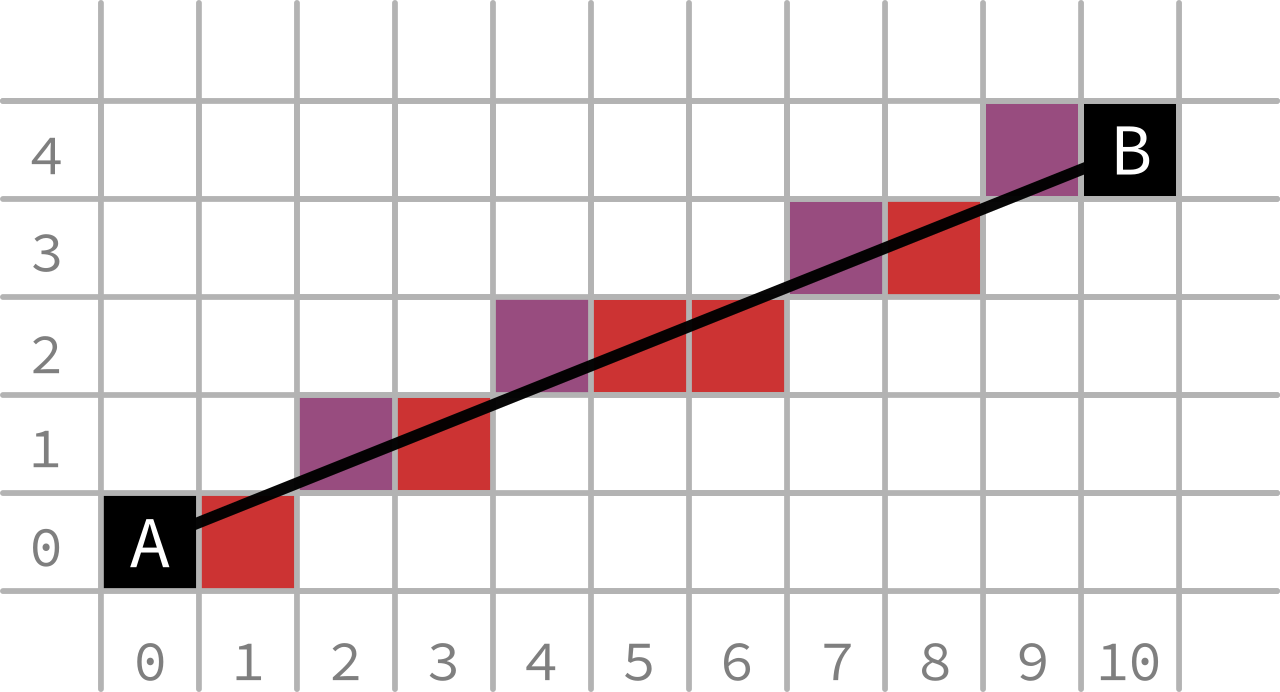
Figure 3: Predominantly horizontal line mapped onto pixel grid

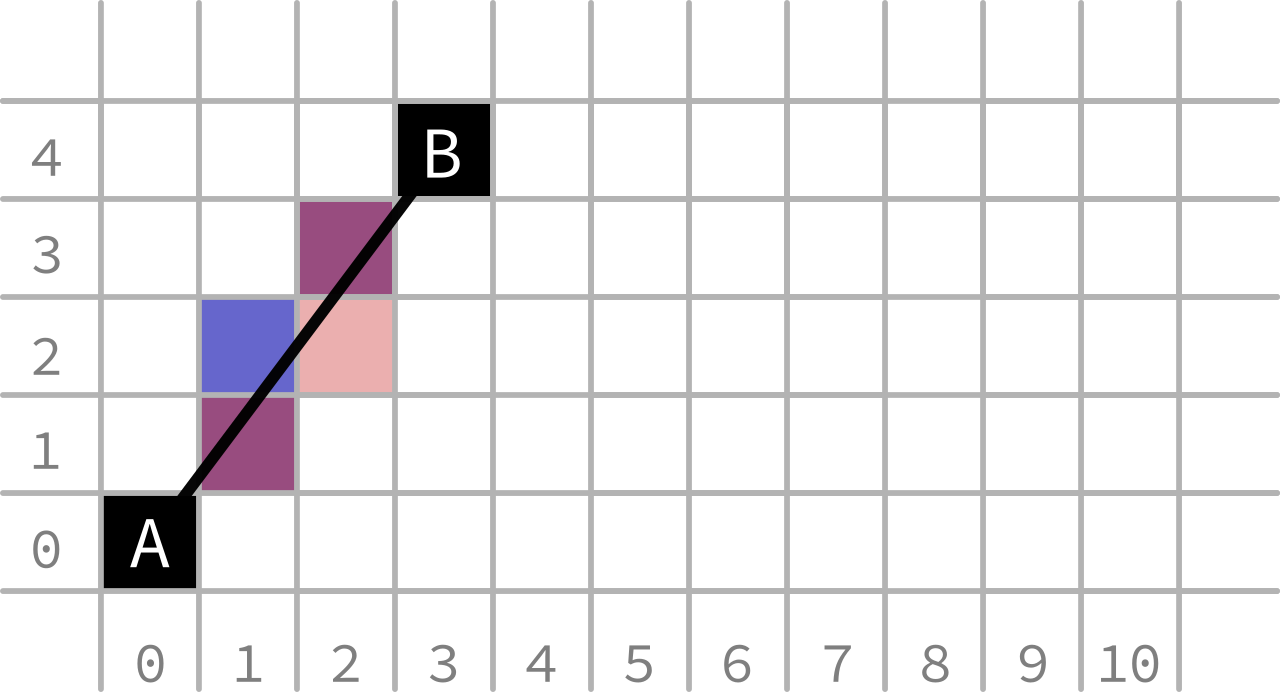
Figure 4: Predominantly vertical line mapped onto pixel grid

The figures above show potential pixels that adequately fit the black line.
They are coloured as in Figure 2 relative to the previous pixel, if moving from A to B.

You can see that an adequate line can be created with the following algorithm:

move 1 in the predominant direction
intersect the line in the non-predominant direction
draw the pixel that the intersection is over
repeat starting from the intersection for the number of pixels in the predominant direction

Shown visually:

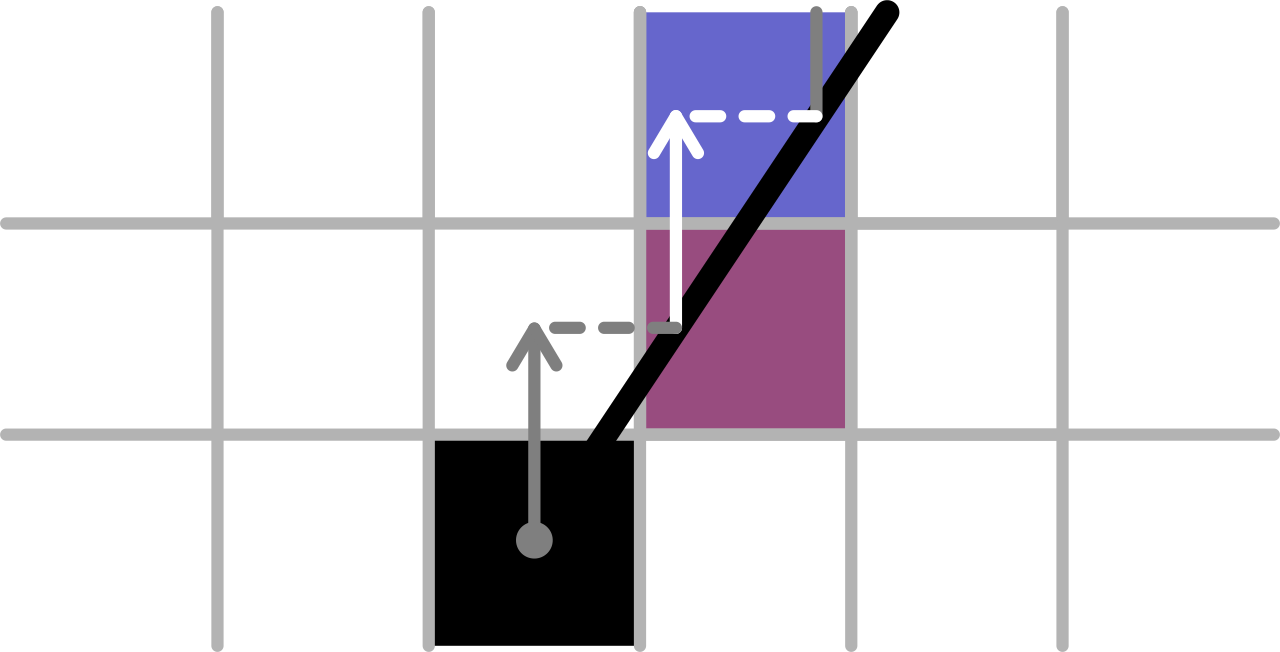
Figure 5: Basic line algorithm

Figure 4 shows a minor issue with this: when the intersection falls on the boundary, the line is weighted slightly towards one point (here the start). This means that a line drawn A-to-B will be slightly different from a line drawn B-to-A. This is not a huge issue, particularly when using a resolution much higher than 10 x 4, but should be easy to special case (see the partially transparent pixel).

It's apparent from Figure 5 that the non-predominant component is both:

less than the predominant component (less than 1)
constant for a given line

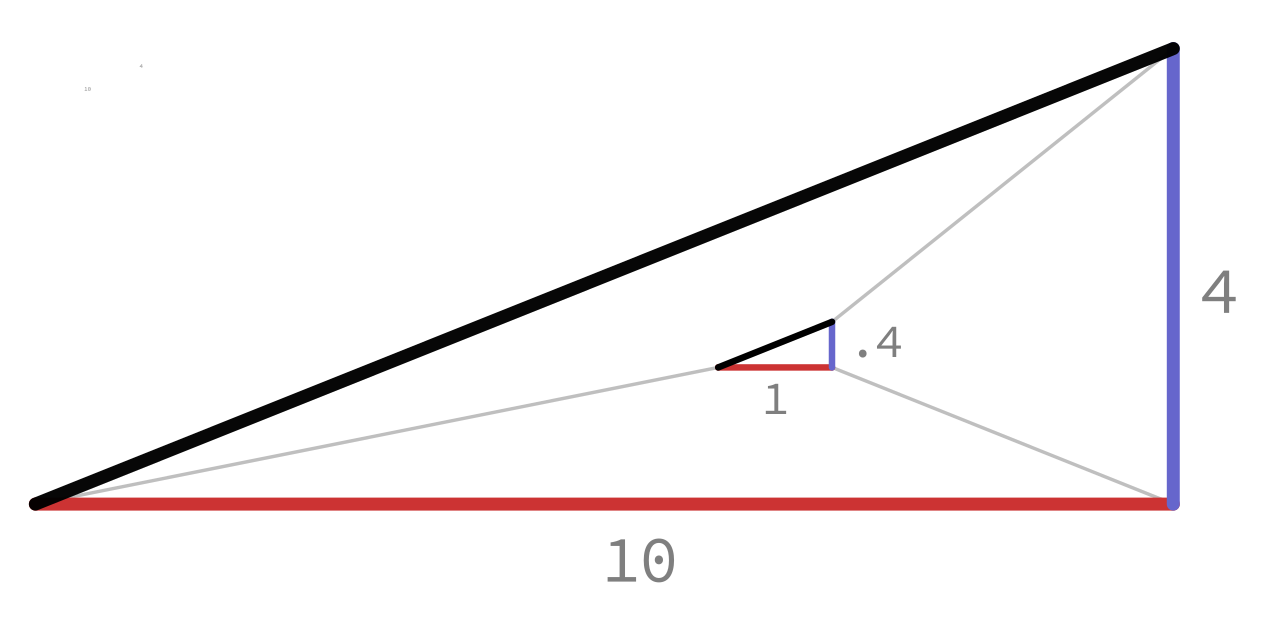
Figure 6: Line components from Figure 2 scaled to pixel size

Implementation of Solution in C:

// 1. Take the buffer to draw in, the 2 points and the colour of the line
/**********************************************************************/

void
DrawLine(image_buffer *Buffer, v2 Point1, v2 Point2, unsigned int Colour)
{

// 2. Find the largest component of AB and divide both compenents by it
/**********************************************************************/

	v2 Dir = V2Sub(Point2, Point1);    // consider the vector from Point1 to Point2
	v2 AbsDir;                         // may have to compare negatives
	AbsDir.X = Abs(Dir.X);
	AbsDir.Y = Abs(Dir.Y);

	float LargestAbsDimension = AbsDir.X;
	if(AbsDir.Y > AbsDir.X)
	{
		LargestAbsDimension = AbsDir.Y;
	}


	v2 SignedDirFraction;
	if(Result.LargestAbsDimension != 0)    // don't divide by 0
	{
		SignedDirFraction.X = Dir.X / LargestAbsDimension;
		SignedDirFraction.Y = Dir.Y / LargestAbsDimension;
	}
	else
	{
		return;    // if the longest side is 0, there is nothing to draw
	}


// 3. Starting from the first point, loop for the number of pixels in the longer dimension, 
//    drawing the pixel, then moving on by the hypotenuse of the component triangle.
/*****************************************************************************************/

	v2 PixelPos = Point1;
	unsigned int LoopCounterEnd = RoundF32ToU32(LargestAbsDimension);
	for(unsigned int LoopCounter = 0;
	    LoopCounter < LoopCounterEnd;
	    ++LoopCounter)
	{
		// Turn 2D floating point coordinate to 1D integral coordinate:
		unsigned int LinearizedPosition = RoundF32ToU32(PixelPos.Y) * Width + RoundF32ToU32(PixelPos.X);
		unsigned int *Pixel = (unsigned int *)Buffer->Memory + LinearizedPosition;
		
		if( (PixelPos.X > 0 && PixelPos.X <= Buffer->Width  - 1 &&    // don't draw outside the screen
		     PixelPos.Y > 0 && PixelPos.Y <= Buffer->Height - 1) )
		{
			*Pixel = Colour;    // no partial transparency, just a simple overwrite
		}

		PixelPos = V2Add(PixelPos, SignedDirFraction);
	}
}

the Wikipedia page

Tom Forsyth's

blog posts

Porter & Duff's original paper on PMA

Conclusion