Implementing a Basic PNG reader the handmade way
First off a couple of rules:
I made the PNG reader purely because when I used "Bitmap Font generator" to try to get a bitmap for some font rendering (as if it wasn't obvious from the name of the program), Bitmap fonts because tackling actual glyph rendering seemed too much of a time killer (i.e: it would take too much to learn everything) I outputted the bitmap image in a PNG format, now if I had chosen a BMP file, this article wouldn't exist because I already have a BMP reader, so once I saw the PNG image, I was like what the hell, let's make a PNG reader, and boy it was fun to both make the code and write this article.
This article is focused on just reading a basic PNG, i.e: single channel (8 bit) image, basically grayscale, but adding the option for reading other types of supported PNG images is merely a matter of some byte manipulation, like reading two bytes instead of one and similar stuff.
1. The Basic Info
PNG files came into being when they decided they wanted to replace GIF images for the go to image file for the web, PNG is a lossless image format, meaning you are not losing any information from the original image (original image here means if you had raw pure pixel data) when compressing the image, unlike jpeg files which go through a different process of compressing the image and lose some info along the way.
The PNG file uses a combination of LZ77 and Huffman Encoding to compress the image, the meat of this article is understanding how those two weave together to make the bulk of the PNG reading code, the other part of the article is the filtering that is applied to each scanline (think rows of pixels) in the image, we will cover both areas in greater detail in a minute.
1.1. The Structure of PNG
The PNG consists of a file signature (8 bytes)
Endians: basically refers to the order in which multibyte data is stored in memory and retrieved. The best way to show this is an example:
imagine memory positions: 0 1 2 3, each position is 1 byte, if the 4 memory locations contain the following 4 hex numbers ( 01 02 03 04 ).
Now remember I didn't say which one of those two endians are right, because I didn't say which system wrote the original memory, if a little endian reads big endian then its wrong and vice versa.
Also know that this only applies to a data that is bigger than one byte and is read and written together, so if you read memory one byte at a time and write them one byte at a time, then it would be the same on both endians, problem only happens when you interpret data that is bigger than one byte.
Because the data in PNG is suppose to be read in big endian, we will write a simple function so that we can read the numbers.
Chunk Type: the chunk type is 4 bytes and each byte has its own meaning, each byte's 5th bit (called property bit) contains a property of the chunk to follow
The standard specifics 18 chunk types, the ordering of the chunks only matter in certain places i.e: a chunk must come before another but doesn't matter where they are, of the 18 chunks only 3 are of important to us for this article, they are the following:
Lets read some chunks
I will use the image below and try to read it into memory

Because the chunks have the same format, lets make a struct for them, and then we can put them into arrays:
Then in the honor of this being "handmade" we define some functions, and macros to help us with life:
Then a function to read one chunk and return its struct:
Now that we have some basic functions so far, we will read 3 chunks, because the PNG i'm using actually only has 3 chunks, an ihdr, idata, and an iend.
for your own images, you would loop until you hit the IEND chunk and then stop, most likely you would have to have a giant IDATA chunk where you have to combine all the data parts of all the IDATA chunks, alas as with most books and articles: "the proof is left for the read as an exercise". (kidding, I will eventually make the 2nd part of this article that tackles some certain cases, but now we move forward my stead).
2. The Fun Part I : The Zlib's Coming
Now assuming we have all the IDATA's data in one place, we will start the decompression journey, as you remember the Zlib structure above, we will start by making a structure for this:
And of course a function to read the Zlib block and return a structure for us (this part could be a little off)
There could potentially be more than one zlib block, unfortunately you cannot get the boundary of those without reading the data and coming to the "end token", we will ge to that.
Fun Part starts here:
You remember how the endian stuff came up in the beginning and it could be confusing for a first timer? yeah, prepare to be even more confused by the zlib stuff, because its actually a "compression" algorithm, it wants to save on bits, yes I repeat "bits" as much as possible, so let's dig into how these bits are laid out in the "bytes".
First off, remove the idea of byte boundary in your head, because once you have everything in memory, numbers and data cross byte boundary all the time, i.e: you have 3 numbers which are only 3 bits each, so that is 9 bits, well that means two bytes, assume the numbers are ( 3, 4, 5 ) in sequence and the numbers would be saved as this:
This means inside the byte, the "data elements" (as the standard calls them) are ordered in a way that the least significant bit is on the right, you start reading from the right, and copy bits into an integer.
But here is the kicker, this applies to data elements that are not huffman codes (we will explain them in a bit), meaning that if you have a data code that is 3 bits, lets say number 3, and then a huffman code that follows it, lets assume the huffman code is (1011, B in hex) then you would get this in the byte:
Confusing as hell I tell ya, but nothing we can't manage, so here is the sum up and what you need to worry about: assume you get a stream of 10 bytes, you take the first byte put it to the far right, and every byte after that go to the left of the first byte, then you start reading from the right by taking bits off, unless you hit a huffman code in which you have to reverse the order of the bits.
i.e: if I tell you take 3 bits off that stream, you would take the first 3 bit on the far right "or" it into an integer and voila you got yourself a valid number except if it's a huffman, you have to read off bits one by one and shift them left.
Because we have to deal with this entire thing as a stream of bits, we will have to make a structure that will keep track of these bits for us and know where it is in stream of bytes, so we have the following structure:
We keep track of bits remaining because we don't track bytes, we track bits, this bit buffer will remove any byte boundary we have, by reading bytes into the buffer and keeping track of how much of it is left, then reading more as needed. the small part to note here is that because pointers can't actually point to bits inside the stream because the smallest possible unit is one byte, this will lead us into moving the stream pointer by byte increments, meaning if we need to read 4 bits, and
there are no bits left, we will take a byte off of the stream, move the stream pointer forward one byte, and put that one byte into our bit buffer then read 4 bits of from it, this means 4 bits will be left. (does that make any sense at all?)
We will make a function that will make sure we have the required number of bits inside bit buffer
We got the bits, now we need a function to read the bits into a reasonable integer:
I will delay the reading of the Huffman codes that require reversing of the bits because we have to get there first.
From now on when I say (n bits) represents that, it means that you read (n bits) using the function above, so something like the first bit is the first bit in the bit_buffer
Okay, now we know how to read bits from the stream, keep track of it and do all of our stuff, now the data we had in the zlib block has a format too, here is how it is:
I'm gonna stop here from explaining the format as I need to explain the deflate algorithm here.
DEFLATE Algorithm
This algorithm actually combines two other algorithms (LZ77 and Huffman coding), so without further ado, here is the explanation for both.
LZ77:
This algorithm is mainly trying to remove duplicates of strings by replacing the duplicate string by a reference to a previous position where the string occurred and a length of the string to duplicate, this is called a back pointer (distance) and length to duplicate.<distance, length> for example this string: hello world my name is bond, hello bond.
When compressed with LZ77 it will become: hello world my name is bond, <29,7><12,4>.
As you can see, the "hello ", yes the space included, occurred again, so it was back referenced to the first occurrence which was 29 bytes before, and starting from 29 bytes back, duplicate 7 bytes (the space is a byte too), then for the bond, it says go back 12 bytes and duplicate 4 bytes, note that because this will be like a stream, when you decompress you must decompress the <29,7> back pointer then decompress the <12, 4> on the result, i.e: you should decompress <29,7> and <12,4> independently.
The main problem of this algorithm? You have to encode the distance, length pair in some way into the stream, meaning when reading the bytes, you must have some idea which one is an actual literal like "hello" and which one is actually a distance, length pair.
One way would be to introduce some form of codes here, an example from the top of my head (could very much be wrong as its 12 AM as I'm writing this) is encode each literal and distance code pair in two bytes, to encode the entire ASCII table you only need one of those bytes, so when you read two bytes, if one of the bytes is completely zero, then its a literal, if both bytes are non zero, you could say the first byte is distance, and the second byte is a length to Duplicate.
Now because people way smarter than me actually made these algorithms, they said oh hell no we won't use two bytes (I was not there to be honest), we will use a variable length of bits and remove the "byte" restriction, thus they said we will use variable lengths of bits to define an "alphabet" for the DEFLATE, the ASCII table is a form of "alphabet" where each symbol in the alphabet uses 8 bits to be represented, so these smart people came up with a better alphabet, in the GZIP alphabet, the first 255 characters (symbols/codes [not very good with the terminology here]) actually still map to the 255 literals of the ASCII table, the 256 symbol/code means "stop token", 257 - 285 indicate "length codes/duplication length", immediately following one of these length codes comes a distance code, see that is the clever part, if you hit a 257-285 code, you know anything after that indicates "distance" code, but wait there is more Cleverness and shenanigans with this algorithm, you see how 285 - 257 = 28 length codes? Well instead of 257 being equal of a length of (1) and 285 being a length of (28), they made those numbers index into a table that indicates whether or not to read more bits for a more flexible number of length codes, i.e: if you get a code of 257 this actually means the length to duplicate is 3, 258 means 4, until 264 means 10 bytes of length to duplicate, but 265 means read one more bit from the stream, if the bit is 0 you have 11 bytes of length, but if its 1 then you have 12 bytes of length, and so on for the other codes after 265, here is the complete table from the standard:
A few more examples: if you get a code of 276, means you read 3 more bits (so decimal number 0 - 7) if the 3 bits are decimal 0, then you have 59 bytes of length to duplicate, if you get 7 then you have length of 66.
So this 255 literals and a 256 stop code with 257-285 length codes are considered one "alphabet", this needs 9 bits to represent this entire "alphabet".
Now after you read the length and any extra needed bits, you get distance codes, which also have their own table and their own actual "alphabet":
See how the code is from 0 to 29?, we need 5 bits to represent those codes (alphabet), so after we hit a code of 264 from the previous alphabet, it indicates we need no extra bits and a length of 10 bytes to duplicate, then after this 264, we read 5 bits, then this 5 bits will map into the distance "alphabet" and indicate the distance to go back e.g: the back pointer to the previous occurrence of the string to duplicate.
if you notice it too, 5 bits means 0 to 31, in this alphabet codes 30 and 31 are never used. And also the codes also indicate how much extra bits you need to read after the 5 bits you just read to get the full distance.
So in conclusion to this part, we need 9 bits to encode the literals/length alphabet and 5 bits to encode the distance alphabet, but wait the smart people said, we wanted to go away from the fixed bit problem, but with this we just changed 8 bit to 9 bit and have 5 bits for these alphabets, so what should we do?
And Huffman Coding comes to the rescue by providing actual variable length encoding for these alphabet, so we won't use full 9 bits for everything and not the entire 5 bits for every distance, we will Huffman Code those stuff.
Huffman Coding:
You remember our problem of having 8 fixed number of bits for our alphabet codes? Well Huffman coding solves that, given some amount of data, the algorithm will assign bit sequences to the elements of the "alphabet" so that they can be uniquely identified even in a stream, it assigned the codes according to frequency of the element appearing in the give data input, i.e: if given a paragraph of text where the letter (which is part of the Alphabet of that paragraph) 'E' has the highest frequency, then the Huffman code will give it the smallest possible code length, and gives the least frequent letter the longest bit length, in our case it could be that the algorithm will give letter 'E' a bit code of (1) where its one bit in length, and maybe the letter 'Z' a 5 bit code like (11011), so why give 'E' a code with bit length of 1? Well because based on the frequency of the letter which appears The most in that input data given, we could assume that it takes up most amount of data in the original input, so the algorithm will assign it the smallest bit length possible to compress it the most.
The algorithm generates "prefix codes" for each element, a Prefix Code means in a set of codes, no one full code will be a prefix to another code, for example take these set of codes [ 1, 2, 3, 4 ], as you see none of the codes in the set are a prefix to one of the other codes, however this set [1, 2, 12, 22], you see that 2 and 1 are complete code on themselves but also are prefix code to the complete codes [12, 22] this will make the code set ambiguous, meaning I can't stream the Data, if I do you will be confused when you see 1 or 2, because it could mean it's either [1 or 2] or start of [12 or 22].
Prefix codes are awesome because they have a property that we need, and that is they can be fully decoded in a stream without the need of a separator, i.e: if you Prefix Code set is [1, 2, 32, 41], when you see a [1] you know it's a full code, and if you see a 4 you know a 1 must follow. Prefix Codes are actually referred to as Huffman Codes even if they are not made by the Huffman algorithm.
The algorithm makes a binary tree, where a leaf nodes indicate alphabet codes and non leaf codes means you still need to take more input in. When you have such a tree, you read inputs bit by bit and follow down the tree, for example, if I have the alphabet of [A, B, C, D], C is the most frequent, then B, then E, then D, then A, then I can make this Huffman tree by assigning them codes like this:
If I give you the stream 10001 with that tree, you know immediately if read from left to right that the stream is CD.
The Huffman in the DEFLATE algorithm has two more restriction on the trees that are generated for the two alphabets that it has, mainly the literal/length codes, and the distance codes, it will encode these two alphabets with different trees, the constraints are these two:
What these two mean is that:
What does those two constrain do for us? well it allows us to reconstruct the entire huffman tree that is used to encode the alphabets just purely by sequentially sending the bit lengths of each code.
we know that the literal/length alphabet starts with 0 and ends with 285, so if I send you a sequence of numbers to indicate the bit lengths like {2, 1, 3, 3, 4, 5}, it means the code for the 0 symbol is 2 bits in length, for 1 is 1 bit in length, for 2 and 3 is three bits in length and so on.
This type of Huffman coding is called Canonical Huffman Coding.
To reconstruct such a tree, you first need the bit length of each of the codes in the tree, then you count the number of times each bit length came up, after that given the two constraints we mentioned, you start assigning codes sequentially and following the two constraints.
An example:
Assume the encoder reencodes the previous example to follow the 2 constraints it will output this;
So if you get the code bit lengths in order, start from A to E, you would get {4, 2, 1, 4, 3}.
Now assume we just received that sequence of bit lengths, we already know the alphabet will be in order so the bit lengths will correspond to the alphabet, so we get the following bit length table
Then we find the maximum bit length that we have, here it's 4, so we only include bit lengths 1 - 4, because there are no bigger bit lengths than 4 , then we compute the number of codes for each bit length, some code for this:
So if we run this code assuming we got the following array
The +1 is there because if the max bit length is 4, and we allocate an array of 4, then the last index of the array would be 3, so we want our array to have an index of 4 available so we add a one to the size, and mostly because we cannot have a bit length of 0
Now code count would be the following
Then we generate the first code for each of the bit lengths that we have (in real world examples the code count will be bigger), the first code of a bit length is one more than the last bit length's final code left shifted by one (add one zero to the right hand side), it means if the last bit length was 2 bits, and the last code for 2 bit length codes was 10 then the first code for 3 bit length codes is (10 + 1 ) << 1 = 110
Now that we have code counts, and their first codes, we will go through everything and assign them codes
Finally that we have assigned codes to each and every element in the alphabet, we can bundle each of these into a neat function and call it (sh_build_huffman_code(uint8 *code_bit_lengths, uint32 len_code_bit_lengths))
and we have our Huffman Tree for the predefined alphabet that we agreed on.

And there we have a huffman tree from the bit lengths of the codes of the alphabet only and nothing else.
Okay, next we need to be able to decode a stream of bits, there are a lot of optimization that goes into this decoding part in real world commertial libraries, but here I will present an extremely simple way to decode a stream, its something like this.
Of course we need some function for these two operations of reading in reverse and decoding
So the DEFLATE algorithm uses both of these algorithm in this way:
Fortunately that is the end of using more Huffman codes to compress data.
Here is the highest level steps in order to decompress the DEFLATE algorithm:
The alphabet of the Huffman Tree that compresses the code bit lengths of the two Huffman trees is number 0 - 18, which have the following meaning:
But there is one thing different about this alphabet, when you read the code bit lengths, the first length isn't for the number 0 as you would expect, it's actually for the number 16, then the next length is for bit 17, then 18, here is the complete list from the standard.
This is because the numbers 16, 17, 18, 0, 8 are very frequent, and the number 15, 1, 14 is not as frequent.
Back On track:
So that now we know how the DEFLATE works, let's get back to the format of this thing, we left of at the 3 bit header, one indicated final bit, and 2 bits indicated type of the method used to build the Huffman tree. we were mainly concerned with the type 10 which is dynamic Huffman tree length
After that 3 bit header, we have these:
After these 14 bits, comes immediately hclen number of 3 bit code lengths that encode the Huffman that is used to compress the other two Huffman trees. (3 bits give you decimal 0 to 7, which is more than enough to encode the code bit lengths for the 0 - 18 alphabet), some code;
we have our tree that has compressed the bit lengths for the other two trees, as you see this tree doesn't have a stop code, so how many symbols must we decode? well we have a total of ( hlit + hdist ) codes we will decode using this tree, after that we can build the two huffman trees and we can decompress the original data.
After this, our two_trees_code_bit_lengths contains the code bit lengths for the two trees, they come one after another, the first one is hlit elements, and the other one is hdist elements, so our two trees are:
Weeheww, we have the two trees now, we can decode the actual data now, lets go.
Decoding now is as simple as just reading symbols of the stream until you hit the stop code (256), and when you hit the stop code if the 'final' bit was not set, you start the whole process again for the next block until you hit the final block. final code for the first part of the Fun.
We need some extra arrays to deal with the distance/length stuff, remember that they need extra bits sometimes, so we will make the following arrays
For the length codes, we have the following two tables, one for extra bits to read, one for the base(starting number) to add the extra bits integer to.
Simply this means that when you get any decoded value between 257 - 285, you basically substract 257 from it to get an index into those two tables.
We know after the length symbol, and the extra bits, comes the distance needed to go back, the distance codes also act like indecies into these two following tables, but the distance codes don't need to be subtracted from any number to get them to map into the tables:
So the final decoding of a zlib block is as follow
If we put all the code so far together, the final decompression function will look like this
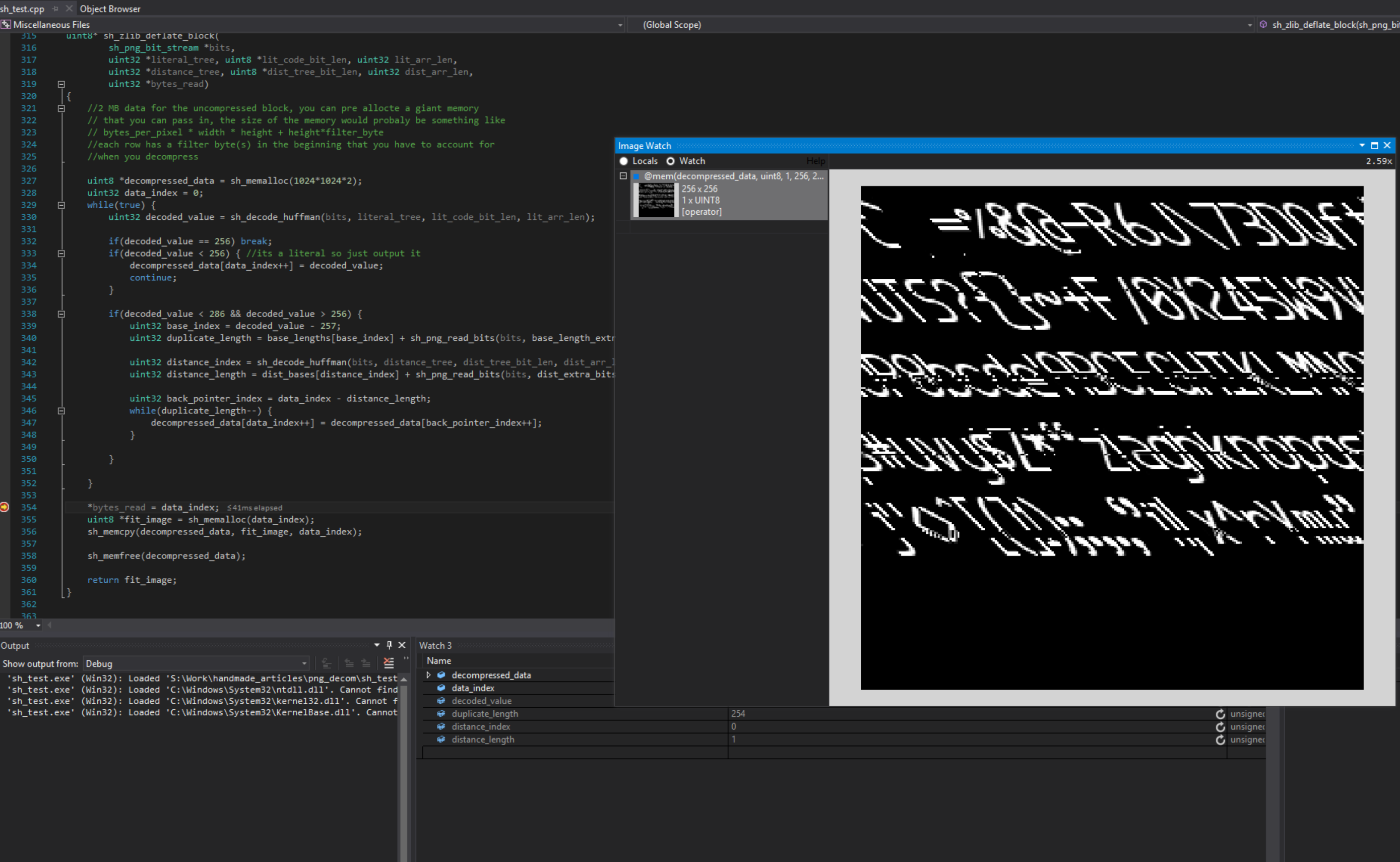
Decompression is Done, now we can do the 2nd fun part and get our image. This is what the image will look like without defiltering it.
3. Part Two: The Final Fun
The second part after we have the decompressed data is that, each row (scanline) in the image is filtered in some way to help with it being compressed, so each row is prefixed with filter bytes that you must read and then apply the appropriate filter to the decompressed data to get back the original image data.
If you remember the filter method field in the IHDR chunk, it says zero, well the standard has only that one filter method, and it defines 5 filter types, they are called in order:
first a simple picture to visualize what the pixel positions we refer to when we talk about filters
Now that we know how the filters work, let's defilter the decompressed image and be done here.
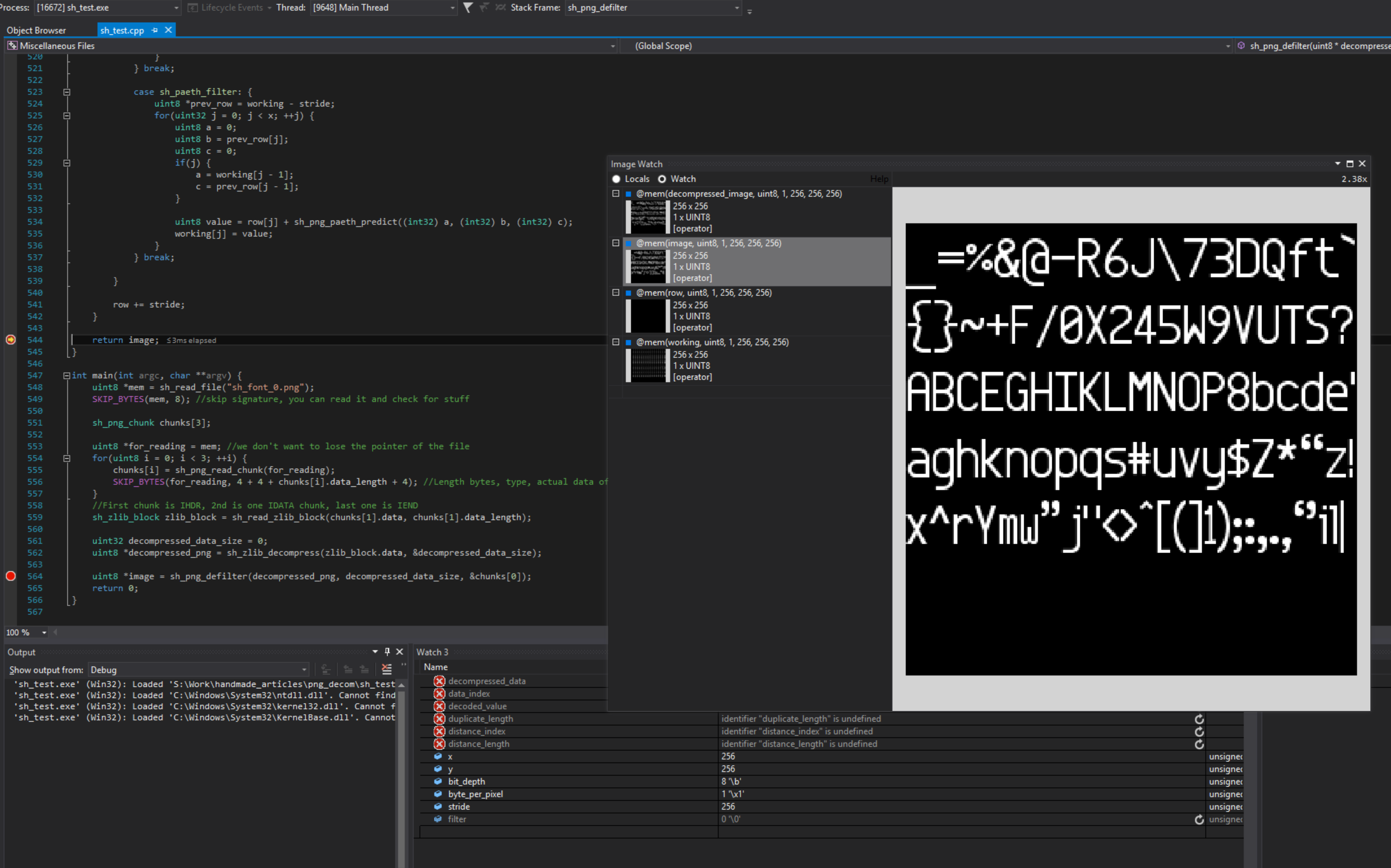
And there you go, we are done, you can now sit back and relax, and you have read a PNG file, you can add other features to it, certainly you can do some error checking, I didn't do any in the code because I want it to be as straight forward as possible.
Here is the final code all in one neat place. you can use it for whatever you like.
I forgot to include a resource that helped me understand the gzip format:
http://commandlinefanatic.com/cgi-bin/showarticle.cgi?article=art001
First off a couple of rules:
- English is not my native language, please do give me feedback on both spelling and grammar
- My first ever article, please do provide feedback in any shape or form
- Code will be as straight forward as possible, it's meant to be easy to understand not optimal, and again, please do provide optimization feed back.
I made the PNG reader purely because when I used "Bitmap Font generator" to try to get a bitmap for some font rendering (as if it wasn't obvious from the name of the program), Bitmap fonts because tackling actual glyph rendering seemed too much of a time killer (i.e: it would take too much to learn everything) I outputted the bitmap image in a PNG format, now if I had chosen a BMP file, this article wouldn't exist because I already have a BMP reader, so once I saw the PNG image, I was like what the hell, let's make a PNG reader, and boy it was fun to both make the code and write this article.
This article is focused on just reading a basic PNG, i.e: single channel (8 bit) image, basically grayscale, but adding the option for reading other types of supported PNG images is merely a matter of some byte manipulation, like reading two bytes instead of one and similar stuff.
1. The Basic Info
PNG files came into being when they decided they wanted to replace GIF images for the go to image file for the web, PNG is a lossless image format, meaning you are not losing any information from the original image (original image here means if you had raw pure pixel data) when compressing the image, unlike jpeg files which go through a different process of compressing the image and lose some info along the way.
The PNG file uses a combination of LZ77 and Huffman Encoding to compress the image, the meat of this article is understanding how those two weave together to make the bulk of the PNG reading code, the other part of the article is the filtering that is applied to each scanline (think rows of pixels) in the image, we will cover both areas in greater detail in a minute.
1.1. The Structure of PNG
The PNG consists of a file signature (8 bytes)
- In hex (89 50 4e 47 0d 0a 1a 0a), this is only to say the file is a PNG.

Then comes a series of chunks, a chunk is just that, a chunk of data of the PNG file, because the PNG was designed to be used on the web, chunking is the obvious way to go. - Length of the chunk data: which is 4 bytes in big endian (will explain this in a bit) and contains the length of the data field of the chunk only, it doesn't include itself, or chunk type, or the crc.

- a 4 byte Header indicating the type of the chunk, called very obviously Chunk Type.
- Actual Chunk Data.
- 4 bytes of CRC32 (big endian again).
- Length of the chunk data: which is 4 bytes in big endian (will explain this in a bit) and contains the length of the data field of the chunk only, it doesn't include itself, or chunk type, or the crc.
Endians: basically refers to the order in which multibyte data is stored in memory and retrieved. The best way to show this is an example:
imagine memory positions: 0 1 2 3, each position is 1 byte, if the 4 memory locations contain the following 4 hex numbers ( 01 02 03 04 ).
- if the system is little endian and you read those 4 bytes into an integer, the integer would be seen as: (04 03 02 01) which is 67305985 in decimal.
- if the system is big endian, and you read those 4 bytes into an integer, the integer would be seen as (01 02 03 04) which is 167345709064 in decimal.
Now remember I didn't say which one of those two endians are right, because I didn't say which system wrote the original memory, if a little endian reads big endian then its wrong and vice versa.
Also know that this only applies to a data that is bigger than one byte and is read and written together, so if you read memory one byte at a time and write them one byte at a time, then it would be the same on both endians, problem only happens when you interpret data that is bigger than one byte.
Because the data in PNG is suppose to be read in big endian, we will write a simple function so that we can read the numbers.
1 2 3 4 5 6 7 8 9 | uint32 sh_get_uint32be(uint8 *mem) {
uint32 result = 0;
for(uint32 i = 0; i < 4; ++i) {
result <<= 8;
result |= *(mem + i);
}
return result;
}
|
Chunk Type: the chunk type is 4 bytes and each byte has its own meaning, each byte's 5th bit (called property bit) contains a property of the chunk to follow
- first byte: if bit is 0: means chunk is critical and required for display of the image, if its 1: means its optional and could potentially be skipped it contains additional info.
- second byte: if bit is 0: public chunk, i.e: internationally and recognized by the standard, if its 1: means its private. (has no functional purpose)
- third byte: reserved for future extension, all bits chunks must have a 1 here.
- fourth byte: this is mostly used by PNG editors not decoders, it indicates whether or not its safe to copy the chunk when the chunk is modified.
The standard specifics 18 chunk types, the ordering of the chunks only matter in certain places i.e: a chunk must come before another but doesn't matter where they are, of the 18 chunks only 3 are of important to us for this article, they are the following:
- IHDR (chunk type bytes: 49 48 44 52): header chunk, contains info about the image, must be the first chunk, it usually is 13 bytes in length, it contains in order:
- 4 bytes, unsigned integer, width, zero is invalid number.
- 4 bytes, unsigned integer, height, zero is invalid number.
- 1 byte , unsigned integer, bit depth, valid values are: 1, 2, 4, 8, 16, number of bits per sample.
- 1 byte , unsigned integer, colour type, PNG image type, valid values are: 0, 2, 3, 4, 6.
- 1 byte , unsigned integer, compression method, only method 0 is defined in the standard, corresponds to DEFLATE algorithm.
- 1 byte , unsigned integer, filter method, only filter type 0 is defined and it has 5 basic filters defined.
- 1 byte , unsigned integer, interlace method, the way the image is transferred, two values defined, 0 (no interlance), 1 (adam7 interlace).
- IDATA (chunk type bytes: 49 44 41 54): actual image data that is compressed, there are multiple of these, they must all come together, which you have combine all together to have the full compressed data.

the data here is basically a (zlib block) compressed data, each zlib block has the following structure. - 1 byte: zlib compression method (named cmf).
- 1 byte: zlib extra flags.
- n byte: actual compressed data.
- 2 bytes: check value, algorithm used is called Adler32.
- IEND (chunk type bytes: 73 69 78 68): the end of the PNG chunks, it "shall be " the chunk to end all the chunks.
- the data part of this chunk is empty, so the data length is zero
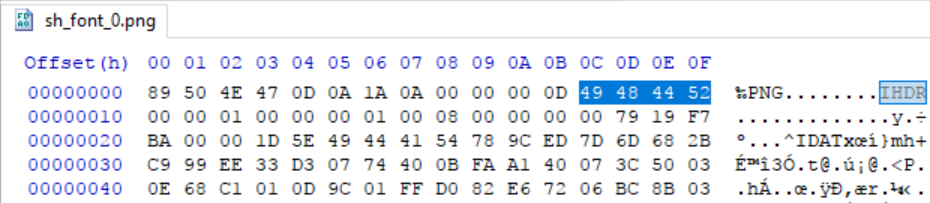
Lets read some chunks
I will use the image below and try to read it into memory

Because the chunks have the same format, lets make a struct for them, and then we can put them into arrays:
1 2 3 4 5 6 | struct sh_png_chunk {
uint32 data_length;
uint8 type[4];
uint8 *data;
uint32 crc32;
}
|
Then in the honor of this being "handmade" we define some functions, and macros to help us with life:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 | //this will just move the pointer by byte_nums forward, or backwards if its negative.
#define SKIP_BYTES(mem, byte_num) (mem += byte_num);
typedef uint8_t uint8;
typedef uint16_t uint16;
typedef uint32_t uint32;
typedef int32_t int32;
uint8* sh_memalloc(uint32 bytes_to_allocate) {
return (uint8 *) HeapAlloc(GetProcessHeap(), HEAP_ZERO_MEMORY, bytes_to_allocate);
}
uint8 sh_memfree(uint8 *mem_pointer) {
return HeapFree(GetProcessHeap(), 0, (LPVOID) mem_pointer);
}
void sh_memcpy(uint8 *from, uint8 *to, uint32 bytes_to_copy) { //copy some bytes from "from" to "to"
while(bytes_to_copy-- > 0) {
*(to + bytes_to_copy) = *(from + bytes_to_copy);
}
}
void sh_memset(uint8 *mem, uint8 value_to_use, uint32 bytes_to_set) {
while(bytes_to_set-- > 0) {
*mem++ = value_to_use;
}
}
uint16 sh_get_uint16be(uint8 *mem) {
uint16 result = 0;
for(uint32 i = 0; i < 2; ++i) {
result <<= 8;
result |= *(mem + i);
}
return result;
}
uint32 sh_get_uint32be(uint8 *mem) {
uint32 result = 0;
for(uint32 i = 0; i < 4; ++i) {
result <<= 8;
result |= *(mem + i);
}
return result;
}
uint8* sh_read_file(const char *file_name) {
uint8 *result = NULL;
HANDLE file = CreateFile(
(const char *)file_name,
GENERIC_READ,
FILE_SHARE_READ,
0,
OPEN_EXISTING,
FILE_ATTRIBUTE_NORMAL,
0
);
DWORD size = GetFileSize(file, 0);
result = sh_memalloc(size);
ReadFile(file, (void *) result, size, 0, 0);
CloseHandle(file);
return result;
}
|
Then a function to read one chunk and return its struct:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
sh_png_chunk sh_png_read_chunk(uint8 *mem) {
sh_png_chunk chunk = {};
chunk.data_length = sh_get_uint32be(mem);
SKIP_BYTES(mem, 4); //we move 4 bytes over because we read the length, which is 4 bytes
*( (uint32 *)&chunk.type) = *((uint32 *) mem);
SKIP_BYTES(mem, 4);
chunk.data = sh_memalloc(chunk.data_length);
sh_memcpy(mem, chunk.data, chunk.data_length);
SKIP_BYTES(mem, chunk.data_length);
chunk.crc32 = sh_get_uint32be(mem);
return chunk;
}
|
Now that we have some basic functions so far, we will read 3 chunks, because the PNG i'm using actually only has 3 chunks, an ihdr, idata, and an iend.
for your own images, you would loop until you hit the IEND chunk and then stop, most likely you would have to have a giant IDATA chunk where you have to combine all the data parts of all the IDATA chunks, alas as with most books and articles: "the proof is left for the read as an exercise". (kidding, I will eventually make the 2nd part of this article that tackles some certain cases, but now we move forward my stead).
2. The Fun Part I : The Zlib's Coming
Now assuming we have all the IDATA's data in one place, we will start the decompression journey, as you remember the Zlib structure above, we will start by making a structure for this:
1 2 3 4 5 6 | struct sh_zlib_block {
uint8 cmf;
uint8 extra_flags;
uint8 *data;
uint16 check_value;
};
|
And of course a function to read the Zlib block and return a structure for us (this part could be a little off)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | sh_zlib_block sh_read_zlib_block(uint8 *mem, uint32 length) {
sh_zlib_block zlib_block = {};
zlib_block.cmf = *mem;
SKIP_BYTES(mem, 1);
zlib_block.extra_flags = *mem;
SKIP_BYTES(mem, 1);
//Length is the sum of all the data, we consumed two bytes, and the last two bytes are for the check value
zlib_block.data = sh_memalloc(length - 2 - 2); //2 for cmf, and flag, 2 for check value
//Remember we already skipped 2 bytes pointer wise, they were for the cmf and flag bytes
sh_memcpy(mem, zlib_block.data, length - 2);
SKIP_BYTES(mem, length - 2);
zlib_block.check_value = sh_get_uint16be(mem);
return zlib_block;
}
|
There could potentially be more than one zlib block, unfortunately you cannot get the boundary of those without reading the data and coming to the "end token", we will ge to that.
Fun Part starts here:
You remember how the endian stuff came up in the beginning and it could be confusing for a first timer? yeah, prepare to be even more confused by the zlib stuff, because its actually a "compression" algorithm, it wants to save on bits, yes I repeat "bits" as much as possible, so let's dig into how these bits are laid out in the "bytes".
First off, remove the idea of byte boundary in your head, because once you have everything in memory, numbers and data cross byte boundary all the time, i.e: you have 3 numbers which are only 3 bits each, so that is 9 bits, well that means two bytes, assume the numbers are ( 3, 4, 5 ) in sequence and the numbers would be saved as this:
1 2 | _ _ _ _ _ _ _ 1 0 1 1 0 0 0 1 1 x x x x x x x 3 2 1 3 2 1 3 2 1 |
This means inside the byte, the "data elements" (as the standard calls them) are ordered in a way that the least significant bit is on the right, you start reading from the right, and copy bits into an integer.
But here is the kicker, this applies to data elements that are not huffman codes (we will explain them in a bit), meaning that if you have a data code that is 3 bits, lets say number 3, and then a huffman code that follows it, lets assume the huffman code is (1011, B in hex) then you would get this in the byte:
1 2 | _ 1 1 0 1 0 1 1
x 1 2 3 4 3 2 1
|
Confusing as hell I tell ya, but nothing we can't manage, so here is the sum up and what you need to worry about: assume you get a stream of 10 bytes, you take the first byte put it to the far right, and every byte after that go to the left of the first byte, then you start reading from the right by taking bits off, unless you hit a huffman code in which you have to reverse the order of the bits.
i.e: if I tell you take 3 bits off that stream, you would take the first 3 bit on the far right "or" it into an integer and voila you got yourself a valid number except if it's a huffman, you have to read off bits one by one and shift them left.
Because we have to deal with this entire thing as a stream of bits, we will have to make a structure that will keep track of these bits for us and know where it is in stream of bytes, so we have the following structure:
1 2 3 4 5 | struct sh_png_bit_stream {
uint8 *data_stream;
uint32 bit_buffer;
uint32 bits_remaining;
}
|
We keep track of bits remaining because we don't track bytes, we track bits, this bit buffer will remove any byte boundary we have, by reading bytes into the buffer and keeping track of how much of it is left, then reading more as needed. the small part to note here is that because pointers can't actually point to bits inside the stream because the smallest possible unit is one byte, this will lead us into moving the stream pointer by byte increments, meaning if we need to read 4 bits, and
there are no bits left, we will take a byte off of the stream, move the stream pointer forward one byte, and put that one byte into our bit buffer then read 4 bits of from it, this means 4 bits will be left. (does that make any sense at all?)
1 2 3 4 5 6 7 | //byte one is the first byte in the data stream you get, not related to how the original data is laid out
byte 1 byte 2
Bit Stream: |10101111| |00101010|
When we read them we read it like this
byte 2 byte 1
Bit Buffer: |00101010| |10101111|
|
We will make a function that will make sure we have the required number of bits inside bit buffer
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | void sh_png_get_bits(sh_png_bit_stream *bits, uint32 bits_required) {
//this is an extremely stupid way to make sure the unsigned integer doesn't underflow, this is just a replacement for abs() but on unsigned integers.
uint32 extra_bits_needed = (bits->bits_remaining > bits_required) ? (bits->bits_remaining - bits_required) : (bits_required - bits->bits_remaining);
uint32 bytes_to_read = extra_bits_needed/8;
//because the above is integer division, there is a possibility of bits to be remaining, i.e: imagine extra_bits_needed is 14, if you do integer division by 8, you get 1, but an extra 6 bits remain
if(extra_bits_needed%8) { //do we have any remaining bits?
//if we do have extra bits they won't be more than 8 bits, so we will add one extra byte for those bits and we are good to go
Bytes_to_read++;
}
for(uint32 i = 0; i < bytes_to_read; ++i) {
uint32 byte = *bits->data_stream++;
bits->bit_buffer |= byte << (i*8 + bits->bits_remaining); //we need to be careful to not overwrite the remaining bits if any
}
bits->bits_remaining += bytes_to_read*8;
}
|
We got the bits, now we need a function to read the bits into a reasonable integer:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | uint32 sh_png_read_bits(sh_png_bit_stream *bits, uint32 bits_to_read) {
uint32 result = 0;
if(bits_to_read > bits->bits_remaining) {
sh_png_get_bits(bits, bits_to_read);
}
for(uint32 i = 0; i < bits_to_read; ++i) {
uint32 bit = bits->bit_buffer & (1 << i);
result |= bit;
}
bits->bit_buffer >>= bits_to_read;
bits->bits_remaining -= bits_to_read;
return result;
}
|
I will delay the reading of the Huffman codes that require reversing of the bits because we have to get there first.
From now on when I say (n bits) represents that, it means that you read (n bits) using the function above, so something like the first bit is the first bit in the bit_buffer
Okay, now we know how to read bits from the stream, keep track of it and do all of our stuff, now the data we had in the zlib block has a format too, here is how it is:
- 3 bit header,
- first bit indicates if the block is the final block (remember how we said it could be multiple blocks? Yeah this tells you if its the last block or not).
- 2 bits indicate the type of the block, indicates the type of the compression used in the block.
- 00 (binary) indicates no compression, so the bits and bytes to follow are not compressed.
- 01 a fixed Huffman code is used (will become clear when we explain the actual Huffman coding stuff)
- 10 a dynamic Huffman code is used
- 11 reserved, means error.
I'm gonna stop here from explaining the format as I need to explain the deflate algorithm here.
DEFLATE Algorithm
This algorithm actually combines two other algorithms (LZ77 and Huffman coding), so without further ado, here is the explanation for both.
LZ77:
This algorithm is mainly trying to remove duplicates of strings by replacing the duplicate string by a reference to a previous position where the string occurred and a length of the string to duplicate, this is called a back pointer (distance) and length to duplicate.<distance, length> for example this string: hello world my name is bond, hello bond.
When compressed with LZ77 it will become: hello world my name is bond, <29,7><12,4>.
As you can see, the "hello ", yes the space included, occurred again, so it was back referenced to the first occurrence which was 29 bytes before, and starting from 29 bytes back, duplicate 7 bytes (the space is a byte too), then for the bond, it says go back 12 bytes and duplicate 4 bytes, note that because this will be like a stream, when you decompress you must decompress the <29,7> back pointer then decompress the <12, 4> on the result, i.e: you should decompress <29,7> and <12,4> independently.
The main problem of this algorithm? You have to encode the distance, length pair in some way into the stream, meaning when reading the bytes, you must have some idea which one is an actual literal like "hello" and which one is actually a distance, length pair.
One way would be to introduce some form of codes here, an example from the top of my head (could very much be wrong as its 12 AM as I'm writing this) is encode each literal and distance code pair in two bytes, to encode the entire ASCII table you only need one of those bytes, so when you read two bytes, if one of the bytes is completely zero, then its a literal, if both bytes are non zero, you could say the first byte is distance, and the second byte is a length to Duplicate.
Now because people way smarter than me actually made these algorithms, they said oh hell no we won't use two bytes (I was not there to be honest), we will use a variable length of bits and remove the "byte" restriction, thus they said we will use variable lengths of bits to define an "alphabet" for the DEFLATE, the ASCII table is a form of "alphabet" where each symbol in the alphabet uses 8 bits to be represented, so these smart people came up with a better alphabet, in the GZIP alphabet, the first 255 characters (symbols/codes [not very good with the terminology here]) actually still map to the 255 literals of the ASCII table, the 256 symbol/code means "stop token", 257 - 285 indicate "length codes/duplication length", immediately following one of these length codes comes a distance code, see that is the clever part, if you hit a 257-285 code, you know anything after that indicates "distance" code, but wait there is more Cleverness and shenanigans with this algorithm, you see how 285 - 257 = 28 length codes? Well instead of 257 being equal of a length of (1) and 285 being a length of (28), they made those numbers index into a table that indicates whether or not to read more bits for a more flexible number of length codes, i.e: if you get a code of 257 this actually means the length to duplicate is 3, 258 means 4, until 264 means 10 bytes of length to duplicate, but 265 means read one more bit from the stream, if the bit is 0 you have 11 bytes of length, but if its 1 then you have 12 bytes of length, and so on for the other codes after 265, here is the complete table from the standard:
1 2 3 4 5 6 7 8 9 10 11 12 13 | Extra Extra Extra Code Bits Length(s) Code Bits Lengths Code Bits Length(s) ---- ---- ------ ---- ---- ------- ---- ---- ------- 257 0 3 267 1 15,16 277 4 67-82 258 0 4 268 1 17,18 278 4 83-98 259 0 5 269 2 19-22 279 4 99-114 260 0 6 270 2 23-26 280 4 115-130 261 0 7 271 2 27-30 281 5 131-162 262 0 8 272 2 31-34 282 5 163-194 263 0 9 273 3 35-42 283 5 195-226 264 0 10 274 3 43-50 284 5 227-257 265 1 11,12 275 3 51-58 285 0 258 266 1 13,14 276 3 59-66 |
A few more examples: if you get a code of 276, means you read 3 more bits (so decimal number 0 - 7) if the 3 bits are decimal 0, then you have 59 bytes of length to duplicate, if you get 7 then you have length of 66.
So this 255 literals and a 256 stop code with 257-285 length codes are considered one "alphabet", this needs 9 bits to represent this entire "alphabet".
Now after you read the length and any extra needed bits, you get distance codes, which also have their own table and their own actual "alphabet":
1 2 3 4 5 6 7 8 9 10 11 12 13 | Extra Extra Extra Code Bits Dist Code Bits Dist Code Bits Distance ---- ---- ---- ---- ---- ------ ---- ---- -------- 0 0 1 10 4 33-48 20 9 1025-1536 1 0 2 11 4 49-64 21 9 1537-2048 2 0 3 12 5 65-96 22 10 2049-3072 3 0 4 13 5 97-128 23 10 3073-4096 4 1 5,6 14 6 129-192 24 11 4097-6144 5 1 7,8 15 6 193-256 25 11 6145-8192 6 2 9-12 16 7 257-384 26 12 8193-12288 7 2 13-16 17 7 385-512 27 12 12289-16384 8 3 17-24 18 8 513-768 28 13 16385-24576 9 3 25-32 19 8 769-1024 29 13 24577-32768 |
See how the code is from 0 to 29?, we need 5 bits to represent those codes (alphabet), so after we hit a code of 264 from the previous alphabet, it indicates we need no extra bits and a length of 10 bytes to duplicate, then after this 264, we read 5 bits, then this 5 bits will map into the distance "alphabet" and indicate the distance to go back e.g: the back pointer to the previous occurrence of the string to duplicate.
if you notice it too, 5 bits means 0 to 31, in this alphabet codes 30 and 31 are never used. And also the codes also indicate how much extra bits you need to read after the 5 bits you just read to get the full distance.
So in conclusion to this part, we need 9 bits to encode the literals/length alphabet and 5 bits to encode the distance alphabet, but wait the smart people said, we wanted to go away from the fixed bit problem, but with this we just changed 8 bit to 9 bit and have 5 bits for these alphabets, so what should we do?
And Huffman Coding comes to the rescue by providing actual variable length encoding for these alphabet, so we won't use full 9 bits for everything and not the entire 5 bits for every distance, we will Huffman Code those stuff.
Huffman Coding:
You remember our problem of having 8 fixed number of bits for our alphabet codes? Well Huffman coding solves that, given some amount of data, the algorithm will assign bit sequences to the elements of the "alphabet" so that they can be uniquely identified even in a stream, it assigned the codes according to frequency of the element appearing in the give data input, i.e: if given a paragraph of text where the letter (which is part of the Alphabet of that paragraph) 'E' has the highest frequency, then the Huffman code will give it the smallest possible code length, and gives the least frequent letter the longest bit length, in our case it could be that the algorithm will give letter 'E' a bit code of (1) where its one bit in length, and maybe the letter 'Z' a 5 bit code like (11011), so why give 'E' a code with bit length of 1? Well because based on the frequency of the letter which appears The most in that input data given, we could assume that it takes up most amount of data in the original input, so the algorithm will assign it the smallest bit length possible to compress it the most.
The algorithm generates "prefix codes" for each element, a Prefix Code means in a set of codes, no one full code will be a prefix to another code, for example take these set of codes [ 1, 2, 3, 4 ], as you see none of the codes in the set are a prefix to one of the other codes, however this set [1, 2, 12, 22], you see that 2 and 1 are complete code on themselves but also are prefix code to the complete codes [12, 22] this will make the code set ambiguous, meaning I can't stream the Data, if I do you will be confused when you see 1 or 2, because it could mean it's either [1 or 2] or start of [12 or 22].
Prefix codes are awesome because they have a property that we need, and that is they can be fully decoded in a stream without the need of a separator, i.e: if you Prefix Code set is [1, 2, 32, 41], when you see a [1] you know it's a full code, and if you see a 4 you know a 1 must follow. Prefix Codes are actually referred to as Huffman Codes even if they are not made by the Huffman algorithm.
The algorithm makes a binary tree, where a leaf nodes indicate alphabet codes and non leaf codes means you still need to take more input in. When you have such a tree, you read inputs bit by bit and follow down the tree, for example, if I have the alphabet of [A, B, C, D], C is the most frequent, then B, then E, then D, then A, then I can make this Huffman tree by assigning them codes like this:
1 2 3 4 5 | 1) A : 0000 2) B : 01 3) C : 1 4) D : 0001 5) E : 001 |
If I give you the stream 10001 with that tree, you know immediately if read from left to right that the stream is CD.
The Huffman in the DEFLATE algorithm has two more restriction on the trees that are generated for the two alphabets that it has, mainly the literal/length codes, and the distance codes, it will encode these two alphabets with different trees, the constraints are these two:
- All codes of a given bit length have lexicographically consecutive values, in the same order as the symbols they represent;
- Shorter codes lexicographically precede longer codes.
What these two mean is that:
- if you have the alphabet, let say: A, B, C, D, and the code of A and B had the same length, i.e: 3 bits, then when sorting the codes lexicographically, the code for A must come before the code of B, so if A is 001 then B must be 010.
- the different bit lengths must come sequential one after another (lexicographically) meaning, if your final 3 bit length code is 010 then the first code for the 4 bit length code is (one plus the last code of the previous bit length left shifted once), meaning ( 010 + 1 ) << 1 so (0110)
What does those two constrain do for us? well it allows us to reconstruct the entire huffman tree that is used to encode the alphabets just purely by sequentially sending the bit lengths of each code.
we know that the literal/length alphabet starts with 0 and ends with 285, so if I send you a sequence of numbers to indicate the bit lengths like {2, 1, 3, 3, 4, 5}, it means the code for the 0 symbol is 2 bits in length, for 1 is 1 bit in length, for 2 and 3 is three bits in length and so on.
This type of Huffman coding is called Canonical Huffman Coding.
To reconstruct such a tree, you first need the bit length of each of the codes in the tree, then you count the number of times each bit length came up, after that given the two constraints we mentioned, you start assigning codes sequentially and following the two constraints.
An example:
Assume the encoder reencodes the previous example to follow the 2 constraints it will output this;
1 2 3 4 5 | 1) A : 1110 2) B : 10 3) C : 0 4) D : 1111 5) E : 110 |
So if you get the code bit lengths in order, start from A to E, you would get {4, 2, 1, 4, 3}.
Now assume we just received that sequence of bit lengths, we already know the alphabet will be in order so the bit lengths will correspond to the alphabet, so we get the following bit length table
1 2 3 4 5 6 | alphabet bit length 1) A 4 2) B 2 3) C 1 4) D 4 5) E 3 |
Then we find the maximum bit length that we have, here it's 4, so we only include bit lengths 1 - 4, because there are no bigger bit lengths than 4 , then we compute the number of codes for each bit length, some code for this:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | uint8 sh_get_maximum_bit_length(uint8 *code_bit_lengths, uint32 len_of_array) {
uint8 max_bit_length = 0;
for(uint32 i = 0; i < len_of_array; ++i) {
if(max_bit_length < code_bit_lengths[i]) {
max_bit_length = code_bit_lengths[i];
}
}
return max_bit_length;
}
void sh_get_bit_length_count(uint32 *code_count, uint8 *code_bit_length, uint32 bit_len_array_len) {
for(uint32 i = 0; i < bit_len_array_len; ++i) {
code_count[code_bit_length[i]]++;
}
}
|
So if we run this code assuming we got the following array
1 2 | uint8 received_code_bit_lengths[] = {4, 2, 1, 4, 3}; //Assume this is what we gotten
uint32 *code_count = sh_memalloc(sizeof(uint32)*( sh_get_maximum_bit_length(received_code_bit_lengths, 5) + 1 ));
|
The +1 is there because if the max bit length is 4, and we allocate an array of 4, then the last index of the array would be 3, so we want our array to have an index of 4 available so we add a one to the size, and mostly because we cannot have a bit length of 0
Now code count would be the following
1 2 3 4 5 | bit length code count 1) 1 1 2) 2 1 3) 3 1 4) 4 2 |
Then we generate the first code for each of the bit lengths that we have (in real world examples the code count will be bigger), the first code of a bit length is one more than the last bit length's final code left shifted by one (add one zero to the right hand side), it means if the last bit length was 2 bits, and the last code for 2 bit length codes was 10 then the first code for 3 bit length codes is (10 + 1 ) << 1 = 110
1 2 3 4 5 6 7 8 9 10 | void sh_first_code_for_bitlen(uint32 *first_codes, uint32 *code_count, uint32 max_bit_length) {
uint32 code = 0;
for(uint32 i = 1; i <= max_bit_length; ++i) {
code = ( code + code_count[i-1]) << 1;
if(code_count[i] > 0) {
first_codes[i] = code;
}
}
}
|
Now that we have code counts, and their first codes, we will go through everything and assign them codes
1 2 3 4 5 6 7 | void sh_assign_Huffman_code(uint32 *assigned_codes, uint32 *first_codes, uint8 *code_bit_lengths, uint32 len_assign_code) {
for(uint32 i = 0; i < len_assign_code; ++i) {
if(code_bit_lengths[i]) {
assigned_codes[i] = first_codes[code_bit_lengths[i]]++;
}
}
}
|
Finally that we have assigned codes to each and every element in the alphabet, we can bundle each of these into a neat function and call it (sh_build_huffman_code(uint8 *code_bit_lengths, uint32 len_code_bit_lengths))
and we have our Huffman Tree for the predefined alphabet that we agreed on.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | uint32* sh_build_huffman_code(uint8 *code_bit_lengths, uint32 len_code_bit_lengths) {
uint32 max_bit_length = sh_get_maximum_bit_length(code_bit_lengths, len_code_bit_lengths);
uint32 *code_counts = (uint32 *)sh_memalloc(sizeof(uint32)*( max_bit_length + 1 ));
uint32 *first_codes = (uint32 *)sh_memalloc(sizeof(uint32)*(max_bit_length + 1));
//we have to assign code to every element in the alphabet, even if we have to assign zero
uint32 *assigned_codes = (uint32 *)sh_memalloc(sizeof(uint32)*(len_code_bit_lengths));
sh_get_bit_length_count(code_counts, code_bit_lengths, len_code_bit_lengths);
//in the real world, when a code of the alphabet has zero bit length, it means it doesn't occur in the data thus we have to reset the count for the zero bit length codes to 0.
code_counts[0] = 0;
sh_first_code_for_bitlen(first_codes, code_counts, max_bit_length);
sh_assign_huffman_code(assigned_codes, first_codes, code_bit_lengths, len_code_bit_lengths);
return assigned_codes;
}
|

And there we have a huffman tree from the bit lengths of the codes of the alphabet only and nothing else.
Okay, next we need to be able to decode a stream of bits, there are a lot of optimization that goes into this decoding part in real world commertial libraries, but here I will present an extremely simple way to decode a stream, its something like this.
- we know every code in the alphabet will be unique to the element of the alphabet and it will have a particular bit length. and we know the stream is made up of these unique codes and there are no ambiguity to them.
- so we will loop through the assigned codes, and then read (and then reverse, remember how the bits were laid out when they were huffman) without consuming the code bit length of the assigned code, for example, if we have this stream (assume its in our bit buffer so we read from the right): 111101110111111
- in our above example we had the following code assignment (copy pasted here so you don't scroll up).
1 2 3 4 5 6
code assigned bit length 1) A : 1110 4 2) B : 10 2 3) C : 0 1 4) D : 1111 4 5) E : 110 3
- if we loop through these, we first read 4 bits because bit length for code A has 4 bits, the first from the right 4 bits of our bit buffer is 1111, then we compare 1111 with 1110, and see they don't match, so the next symbol is not A.
for B, we read two bits, which means (11), which is not 10, for C the one bit we read is (1) so not C either, once we hit D, we read 4 bits, its 1111 and voila, the symbol is decoded, now we consume 4 bits and we are left with: 11110111011 - if we read 4 bits (and reverse them), we get 1101, which is not equal to 1110, so its not A, for B its (11), so not B either, for C its (1), not C either, for D its (1101), not D either, for E its (110), and voila next symbol is E, so we consume 3 bits, left with: 11110111
- for A its (1110), so its symbol is A, then we are left with: 1111, which is D, and we got the decoded stream as DEAD.
- if we loop through these, we first read 4 bits because bit length for code A has 4 bits, the first from the right 4 bits of our bit buffer is 1111, then we compare 1111 with 1110, and see they don't match, so the next symbol is not A.
Of course we need some function for these two operations of reading in reverse and decoding
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | uint32 sh_peak_bits_reverse(sh_png_bit_stream *bits, uint32 bits_to_peak) {
if(bits_to_peak > bits->bits_remaining) {
sh_png_get_bits(bits, bits_to_peak);
}
uint32 result = 0; //this could potentially cause problems,
for(uint32 i = 0; i < bits_to_peak; ++i) {
result <<= 1;
uint32 bit = bits->bit_buffer & (1 << i);
result |= (bit > 0) ? 1 : 0;
}
return result;
}
uint32 sh_decode_Huffman(sh_png_bit_stream *bits, uint32 *assigned_codes, uint8 *code_bit_lengths, uint32 assigned_code_length) {
for(uint32 i = 0; i < assigned_code_length; ++i) {
uint32 code = sh_peak_bits_reverse(bits, code_bit_lengths[i]);
if(assigned_codes[i] == code) {
bits->bit_buffer >>= code_bit_lengths[i];
bits->bits_remaining -= code_bit_lengths[i];
return i;
}
}
return 0;
}
|
So the DEFLATE algorithm uses both of these algorithm in this way:
- use LZ77 to compress the original data.
- use Huffman Coding to compress the LZ77 of the original data. this will produce the ( two trees ), one for the Literals/Length codes, one for the distance codes. we only need code bit lengths from these two trees to reconstruct the trees.
- use another Huffman Code Pass to compress the Huffman Trees (only the bit lengths of the codes) for the Compression of the LZ77 compression of the original data. we only need the code bit lengths from this tree too. This tree has its own alphabet too as we will see shortly
Fortunately that is the end of using more Huffman codes to compress data.
Here is the highest level steps in order to decompress the DEFLATE algorithm:
- Read the code bit lengths for the code bit lengths of the two trees, and Build a Huffman tree.
- Decode the two tree code bit lengths using the Huffman Tree from step one.
- Now that we have the code bit length's for the two trees, use them to reconstruct the two trees.
- Use the two Huffman Trees from the previous step to decompress the LZ77 code and get the original data back.
The alphabet of the Huffman Tree that compresses the code bit lengths of the two Huffman trees is number 0 - 18, which have the following meaning:
- codes 0 to 15: they represent literal code bit lengths, i.e: if you see number 15 it means the code bit length is 15 bits long. 15 is the maximum because that is the longest a code bit length can be in when making the "two trees"
- code 16: means repeat the previous code 3 to 6 times depending on the next 2 bits. So if you get number 16, you read 2 more bits and interpret them as an integer (2 bits only mean decimal 0 to 3) then add them to the number 3.
- code 17: means repeat 0 for 3 - 10 times depending on the next 3 bits. if you see 17, read the next 3 bits and add the integer to the number 3 and you get repeat count.
- code 18: means repeat 0 for 11 - 138 times depending on the next 7 bits. if you see 18, read the next 7 bits and add the integer to the number 11 and you get repeat count.
But there is one thing different about this alphabet, when you read the code bit lengths, the first length isn't for the number 0 as you would expect, it's actually for the number 16, then the next length is for bit 17, then 18, here is the complete list from the standard.
1 | 16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15 |
This is because the numbers 16, 17, 18, 0, 8 are very frequent, and the number 15, 1, 14 is not as frequent.
Back On track:
So that now we know how the DEFLATE works, let's get back to the format of this thing, we left of at the 3 bit header, one indicated final bit, and 2 bits indicated type of the method used to build the Huffman tree. we were mainly concerned with the type 10 which is dynamic Huffman tree length
After that 3 bit header, we have these:
- 5 bits called hlit: the number of literals/length codes - 257, so when you read this 5 bits, interpret it as integer then add 257 to it (remember the tree must encode all the literals and the stop code)
- 5 bits called hdist: the number of distance codes - 1, you read 5 bits then add one to the integer.
- 4 bits called hclen, number of length codes that are used to encode the Huffman tree that will encode the other 2 trees - 4. So you read 4 bits and add 4 to it (remember the alphabet used to compress the two tree length codes, the 0 - 18 one? Well the reason for the +4 is that you need at minimum encode the repetitions and the length for the zero).
After these 14 bits, comes immediately hclen number of 3 bit code lengths that encode the Huffman that is used to compress the other two Huffman trees. (3 bits give you decimal 0 to 7, which is more than enough to encode the code bit lengths for the 0 - 18 alphabet), some code;
1 2 3 4 5 6 7 8 | uint8 code_lengths_of_code_length_order[] = {16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15};
uint8 code_length_of_code_length[19]; //maximum alphabet symbol is 18
for(uint8 i = 0; i < hclen; ++i) {
code_length_of_code_length[code_lengths_of_code_length_order[i]] = sh_png_read_bits(bits, 3);
}
uint32 *huffman_codes_of_tree_of_trees = sh_build_huffman_code(code_length_of_code_length, 19);
|
we have our tree that has compressed the bit lengths for the other two trees, as you see this tree doesn't have a stop code, so how many symbols must we decode? well we have a total of ( hlit + hdist ) codes we will decode using this tree, after that we can build the two huffman trees and we can decompress the original data.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | uint8 *two_trees_code_bit_lengths = sh_memalloc(hlit + hdist);
//because we have repetition, we won't necessarly have the exact bit lengths for each symbol if we just loop one increment at a time
uint32 code_index = 0;
while(code_index < (hdist+hlit)) {
uint32 decoded_value = sh_decode_huffman(bits, huffman_codes_of_tree_of_trees, code_length_of_code_length, 19);
if(decoded_value < 16) {
two_trees_code_bit_lengths[code_index++] = decoded_value;
continue;
}
uint32 repeat_count = 0;
uint8 code_length_to_repeat = 0;
switch(decoded_value) {
case 16:
repeat_count = sh_png_read_bits(bits, 2) + 3;// 3 - 6 repeat count
code_length_to_repeat = two_trees_code_bit_lengths[code_index - 1];
break;
case 17:
repeat_count = sh_png_read_bits(bits, 3) + 3;// 3 - 10 repeat count
break;
case 18:
repeat_count = sh_png_read_bits(bits, 7) + 11;// 3 - 10 repeat count
break;
}
sh_memset(two_trees_code_bit_lengths + code_index, code_length_to_repeat, repeat_count);
code_index += repeat_count;
}
|
After this, our two_trees_code_bit_lengths contains the code bit lengths for the two trees, they come one after another, the first one is hlit elements, and the other one is hdist elements, so our two trees are:
1 2 | uint32 *literal_length_huff_tree = sh_build_huffman_code(two_trees_code_bit_lengths, hlit); uint32 *distance_huff_tree = sh_build_huffman_code(two_trees_code_bit_lengths + hlit, hdist); |
Weeheww, we have the two trees now, we can decode the actual data now, lets go.
Decoding now is as simple as just reading symbols of the stream until you hit the stop code (256), and when you hit the stop code if the 'final' bit was not set, you start the whole process again for the next block until you hit the final block. final code for the first part of the Fun.
We need some extra arrays to deal with the distance/length stuff, remember that they need extra bits sometimes, so we will make the following arrays
For the length codes, we have the following two tables, one for extra bits to read, one for the base(starting number) to add the extra bits integer to.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | uint8 base_length_extra_bit[] = {
0, 0, 0, 0, 0, 0, 0, 0, //257 - 264
1, 1, 1, 1, //265 - 268
2, 2, 2, 2, //269 - 273
3, 3, 3, 3, //274 - 276
4, 4, 4, 4, //278 - 280
5, 5, 5, 5, //281 - 284
0 //285
};
uint32 base_lengths[] = {
3, 4, 5, 6, 7, 8, 9, 10, //257 - 264
11, 13, 15, 17, //265 - 268
19, 23, 27, 31, //269 - 273
35, 43, 51, 59, //274 - 276
67, 83, 99, 115, //278 - 280
131, 163, 195, 227, //281 - 284
258 //285
};
|
Simply this means that when you get any decoded value between 257 - 285, you basically substract 257 from it to get an index into those two tables.
We know after the length symbol, and the extra bits, comes the distance needed to go back, the distance codes also act like indecies into these two following tables, but the distance codes don't need to be subtracted from any number to get them to map into the tables:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | uint32 dist_bases[] = {
/*0*/ 1, 2, 3, 4, //0-3
/*1*/ 5, 7, //4-5
/*2*/ 9, 13, //6-7
/*3*/ 17, 25, //8-9
/*4*/ 33, 49, //10-11
/*5*/ 65, 97, //12-13
/*6*/ 129, 193, //14-15
/*7*/ 257, 385, //16-17
/*8*/ 513, 769, //18-19
/*9*/ 1025, 1537, //20-21
/*10*/ 2049, 3073, //22-23
/*11*/ 4097, 6145, //24-25
/*12*/ 8193, 12289, //26-27
/*13*/ 16385, 24577 //28-29
0 , 0 //30-31, error, shouldn't occur
};
uint32 dist_extra_bits[] = {
/*0*/ 0, 0, 0, 0, //0-3
/*1*/ 1, 1, //4-5
/*2*/ 2, 2, //6-7
/*3*/ 3, 3, //8-9
/*4*/ 4, 4, //10-11
/*5*/ 5, 5, //12-13
/*6*/ 6, 6, //14-15
/*7*/ 7, 7, //16-17
/*8*/ 8, 8, //18-19
/*9*/ 9, 9, //20-21
/*10*/ 10, 10, //22-23
/*11*/ 11, 11, //24-25
/*12*/ 12, 12, //26-27
/*13*/ 13, 13 //28-29
0 , 0 //30-31 error, they shouldn't occur
};
|
So the final decoding of a zlib block is as follow
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | uint8* sh_zlib_deflate_block(
sh_png_bit_stream *bits,
uint32 *literal_tree, uint8 *lit_code_bit_len, uint32 lit_arr_len,
uint32 *distance_tree, uint8 *dist_tree_bit_len, uint32 dist_arr_len,
uint32 *bytes_read)
{
//1 MB data for the uncompressed block, you can pre allocate a giant memory
// that you can pass in, the size of the memory would probably be something like
// bytes_per_pixel * width * height + height*filter_byte
//each row has a filter byte(s) in the beginning that you have to account for
//when you decompress
uint8 *decompressed_data = sh_memalloc(1024*1024);
uint32 data_index = 0;
while(true) {
uint32 decoded_value = sh_decode_huffman(bits, literal_tree, lit_code_bit_len, lit_arr_len);
if(decoded_value == 256) break;
if(decoded_value < 256) { //its a literal so just output it
decompressed_data[data_index++] = decoded_value;
continue;
}
if(decoded_value < 286 && decoded_value > 256) {
uint32 base_index = decoded_value - 257;
uint32 duplicate_length = base_lengths[base_index] + sh_png_read_bits(bits, base_length_extra_bit[base_index]);;
uint32 distance_index = sh_decode_Huffman(bits, distance_tree, dist_tree_bit_len, dist_arr_len);
uint32 distance_length = dist_bases[distance_index] + sh_png_read_bits(bits, dist_extra_bits[distance_index]);
uint32 back_pointer_index = data_index - distance_length;
while(duplicate_length--) {
decompressed_data[Data_index++] = decompressed_data[back_pointer_index++];
}
}
}
*bytes_read = data_index;
uint8 *fit_image = sh_memalloc(data_index);
sh_memcpy(decompressed_data, fit_image, data_index);
sh_memfree(decompressed_data);
return fit_image;
}
|
If we put all the code so far together, the final decompression function will look like this
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 | uint8* sh_zlib_decompress(uint8 *zlib_data, uint32 *decompressed_size) {
uint8 *decompressed_data = sh_memalloc(1024*1024*4); //4 MB free space
uint32 data_read = 0;
uint32 final;
uint32 type;
sh_png_bit_stream bit_stream = {zlib_data, 0, 0};
sh_png_bit_stream *bits = &bit_stream;
do {
final = sh_png_read_bits(bits, 1);
type = sh_png_read_bits(bits, 2);
uint32 hlit = sh_png_read_bits(bits, 5) + 257;
uint32 hdist = sh_png_read_bits(bits, 5) + 1;
uint32 hclen = sh_png_read_bits(bits, 4) + 4;
uint8 code_lengths_of_code_length_order[] = {16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15};
uint8 code_length_of_code_length[19]; //maximum alphabet symbol is 18
sh_memset(code_length_of_code_length, 0, 19);
for(uint8 i = 0; i < hclen; ++i) {
code_length_of_code_length[code_lengths_of_code_length_order[i]] = sh_png_read_bits(bits, 3);
}
uint32 *huffman_codes_of_tree_of_trees = sh_build_huffman_code(code_length_of_code_length, 19);
uint8 *two_trees_code_bit_lengths = sh_memalloc(hlit + hdist);
//because we have repetition, we won't necessarily have one to one mapping for bit lengths for each symbol encoded.
uint32 code_index = 0;
while(code_index < (hdist+hlit)) {
uint32 decoded_value = sh_decode_huffman(bits, huffman_codes_of_tree_of_trees, code_length_of_code_length, 19);
if(decoded_value < 16) {
two_trees_code_bit_lengths[code_index++] = decoded_value;
continue;
}
uint32 repeat_count = 0;
uint8 code_length_to_repeat = 0;
switch(decoded_value) {
case 16:
repeat_count = sh_png_read_bits(bits, 2) + 3;// 3 - 6 repeat count
code_length_to_repeat = two_trees_code_bit_lengths[code_index - 1];
break;
case 17:
repeat_count = sh_png_read_bits(bits, 3) + 3;// 3 - 10 repeat count
break;
case 18:
repeat_count = sh_png_read_bits(bits, 7) + 11;// 3 - 10 repeat count
break;
}
sh_memset(two_trees_code_bit_lengths + code_index, code_length_to_repeat, repeat_count);
code_index += repeat_count;
}
uint32 *literal_length_huff_tree = sh_build_huffman_code(two_trees_code_bit_lengths, hlit);
uint32 *distance_huff_tree = sh_build_huffman_code(two_trees_code_bit_lengths + hlit, hdist);
uint32 block_size = 0;
uint8 *decompressed_block = sh_zlib_deflate_block(
bits,
literal_length_huff_tree, two_trees_code_bit_lengths, hlit,
distance_huff_tree, two_trees_code_bit_lengths + hlit, hdist,
&block_size);
sh_memcpy(decompressed_block, decompressed_data + data_read, block_size);
data_read += block_size;
sh_memfree(decompressed_block);
} while(!final);
*decompressed_size = data_read;
return decompressed_data;
}
|
Decompression is Done, now we can do the 2nd fun part and get our image. This is what the image will look like without defiltering it.

3. Part Two: The Final Fun
The second part after we have the decompressed data is that, each row (scanline) in the image is filtered in some way to help with it being compressed, so each row is prefixed with filter bytes that you must read and then apply the appropriate filter to the decompressed data to get back the original image data.
If you remember the filter method field in the IHDR chunk, it says zero, well the standard has only that one filter method, and it defines 5 filter types, they are called in order:
first a simple picture to visualize what the pixel positions we refer to when we talk about filters
- None, the row is not filtered, you just remove the filter byte and copy it untouched.
- Sub, the filtered pixel is the difference between the current pixel and the previous pixel on the same scanline (a)
- Up, the filtered pixel is the difference between the current pixel and the pixel above it (b), i.e: the same pixel position in the previous scanline
- average, the filtered pixel is the average between the (a) pixel and (b) pixel.
- Paeth, a filter a guy came up (pretty smart guy), basically it's the difference between the current pixel and the PaethPredictor pixel. Here is the Paeth Algorithm
1 2 3 4 5 6 7 8 9 10
int32 sh_png_paeth_predict(int32 a, int32 b, int32 c) { int32 p = a + b - c; int32 pa = sh_abs(p - a); int32 pb = sh_abs(p - b); int32 pc = sh_abs(p - c); if(pa <= pb && pa <= pc) return a; if(pb <= pc) return b; return c; }
Now that we know how the filters work, let's defilter the decompressed image and be done here.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 | enum sh_png_filters { sh_no_filter, sh_sub_filter, sh_up_filter, sh_avg_filter, sh_paeth_filter }; uint8* sh_png_defilter(uint8 *decompressed_image, uint32 size, sh_png_chunk *ihdr) { uint32 x = sh_get_uint32be(ihdr->data); uint32 y = sh_get_uint32be(ihdr->data+4); uint8 bit_depth = *( ihdr->data + 4 + 4 );//count the bytes out //this is usually determined by checking color type, the picture I'm using is only grayscale, its only one byte per pixel uint8 byte_per_pixel = 1; uint8 *row = decompressed_image; uint32 stride = x*byte_per_pixel; uint8 *image = sh_memalloc(x*y*byte_per_pixel); //this is even smaller than the filter but just being safe uint8 *working = image; for(uint32 i = 0; i < y; ++i) { working = image + i*stride; uint8 filter = *row++; switch(filter) { case sh_no_filter: { for(uint32 j = 0; j < x; ++j) { working[j] = row[j]; } } break; case sh_sub_filter: { for(uint32 j = 0; j < x; ++j) { uint8 a = 0; if(j != 0) { a = working[j-1]; } uint8 value = row[j] + a; working[j] = value; } } break; case sh_up_filter: { uint8 *prev_row = working - stride; for(uint32 j = 0; j < x; ++j) { uint8 b = prev_row[j]; uint8 value = row[j] + b; working[j] = value; } } break; case sh_avg_filter: { uint8 *prev_row = working - stride; for(uint32 j = 0; j < x; ++j) { uint8 a = 0; uint8 b = prev_row[j]; if(j) { a = working[j - 1]; } uint8 value = row[j] + ( (a + b) >> 1 ); working[j] = value; } } break; case sh_paeth_filter: { uint8 *prev_row = working - stride; for(uint32 j = 0; j < x; ++j) { uint8 a = 0; uint8 b = prev_row[j]; uint8 c = 0; if(j) { a = working[j - 1]; c = prev_row[j - 1]; } uint8 value = row[j] + sh_png_paeth_predict((int32) a, (int32) b, (int32) c); working[j] = value; } } break; } row += stride; } return image; } |

And there you go, we are done, you can now sit back and relax, and you have read a PNG file, you can add other features to it, certainly you can do some error checking, I didn't do any in the code because I want it to be as straight forward as possible.
Here is the final code all in one neat place. you can use it for whatever you like.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 | #include <Windows.h> #include <stdint.h> typedef uint8_t uint8; typedef uint16_t uint16; typedef uint32_t uint32; typedef int32_t int32; #define SKIP_BYTES(mem, bytes_to_skip) (mem += bytes_to_skip) int32 sh_abs(int32 number) { return (number > 0) ? number : -1*number; } uint8 base_length_extra_bit[] = { 0, 0, 0, 0, 0, 0, 0, 0, //257 - 264 1, 1, 1, 1, //265 - 268 2, 2, 2, 2, //269 - 273 3, 3, 3, 3, //274 - 276 4, 4, 4, 4, //278 - 280 5, 5, 5, 5, //281 - 284 0 //285 }; uint32 base_lengths[] = { 3, 4, 5, 6, 7, 8, 9, 10, //257 - 264 11, 13, 15, 17, //265 - 268 19, 23, 27, 31, //269 - 273 35, 43, 51, 59, //274 - 276 67, 83, 99, 115, //278 - 280 131, 163, 195, 227, //281 - 284 258 //285 }; uint32 dist_bases[] = { /*0*/ 1, 2, 3, 4, //0-3 /*1*/ 5, 7, //4-5 /*2*/ 9, 13, //6-7 /*3*/ 17, 25, //8-9 /*4*/ 33, 49, //10-11 /*5*/ 65, 97, //12-13 /*6*/ 129, 193, //14-15 /*7*/ 257, 385, //16-17 /*8*/ 513, 769, //18-19 /*9*/ 1025, 1537, //20-21 /*10*/ 2049, 3073, //22-23 /*11*/ 4097, 6145, //24-25 /*12*/ 8193, 12289, //26-27 /*13*/ 16385, 24577, //28-29 0 , 0 //30-31, error, shouldn't occur }; uint32 dist_extra_bits[] = { /*0*/ 0, 0, 0, 0, //0-3 /*1*/ 1, 1, //4-5 /*2*/ 2, 2, //6-7 /*3*/ 3, 3, //8-9 /*4*/ 4, 4, //10-11 /*5*/ 5, 5, //12-13 /*6*/ 6, 6, //14-15 /*7*/ 7, 7, //16-17 /*8*/ 8, 8, //18-19 /*9*/ 9, 9, //20-21 /*10*/ 10, 10, //22-23 /*11*/ 11, 11, //24-25 /*12*/ 12, 12, //26-27 /*13*/ 13, 13, //28-29 0 , 0 //30-31 error, they shouldn't occur }; struct sh_png_chunk { uint32 data_length; uint8 type[4]; uint8 *data; uint32 crc32; }; struct sh_zlib_block { uint8 cmf; uint8 extra_flags; uint8 *data; uint16 check_value; }; struct sh_png_bit_stream { uint8 *data_stream; uint32 bit_buffer; uint32 bits_remaining; }; enum sh_png_filters { sh_no_filter, sh_sub_filter, sh_up_filter, sh_avg_filter, sh_paeth_filter }; uint8* sh_memalloc(uint32 bytes_to_allocate) { return (uint8 *) HeapAlloc(GetProcessHeap(), HEAP_ZERO_MEMORY, bytes_to_allocate); } uint8 sh_memfree(uint8 *mem_pointer) { return HeapFree(GetProcessHeap(), 0, (LPVOID) mem_pointer); } void sh_memcpy(uint8 *from, uint8 *to, uint32 bytes_to_copy) { //copy some bytes from "from" to "to" while(bytes_to_copy-- > 0) { *(to + bytes_to_copy) = *(from + bytes_to_copy); } } void sh_memset(uint8 *mem, uint8 value_to_use, uint32 bytes_to_set) { while(bytes_to_set-- > 0) { *mem++ = value_to_use; } } uint16 sh_get_uint16be(uint8 *mem) { uint16 result = 0; for(uint32 i = 0; i < 2; ++i) { result <<= 8; result |= *(mem + i); } return result; } uint32 sh_get_uint32be(uint8 *mem) { uint32 result = 0; for(uint32 i = 0; i < 4; ++i) { result <<= 8; result |= *(mem + i); } return result; } uint8* sh_read_file(const char *file_name) { uint8 *result = NULL; HANDLE file = CreateFile( (const char *)file_name, GENERIC_READ, FILE_SHARE_READ, 0, OPEN_EXISTING, FILE_ATTRIBUTE_NORMAL, 0 ); DWORD size = GetFileSize(file, 0); result = sh_memalloc(size); ReadFile(file, (void *) result, size, 0, 0); CloseHandle(file); return result; } sh_png_chunk sh_png_read_chunk(uint8 *mem) { sh_png_chunk chunk = {}; chunk.data_length = sh_get_uint32be(mem); SKIP_BYTES(mem, 4); //we move 4 bytes over because we read the length, which is 4 bytes *( (uint32 *)&chunk.type) = *((uint32 *) mem); SKIP_BYTES(mem, 4); chunk.data = sh_memalloc(chunk.data_length); sh_memcpy(mem, chunk.data, chunk.data_length); SKIP_BYTES(mem, chunk.data_length); chunk.crc32 = sh_get_uint32be(mem); return chunk; } sh_zlib_block sh_read_zlib_block(uint8 *mem, uint32 length) { sh_zlib_block zlib_block = {}; zlib_block.cmf = *mem; SKIP_BYTES(mem, 1); zlib_block.extra_flags = *mem; SKIP_BYTES(mem, 1); //Length is the sum of all the data, we consumed two bytes, and the last two bytes are for the check value zlib_block.data = sh_memalloc(length - 2 - 2); //2 for cmf, and flag, 2 for check value //Remember we already skipped 2 bytes pointer wise, they were for the cmf and flag bytes sh_memcpy(mem, zlib_block.data, length - 2); SKIP_BYTES(mem, length - 2); zlib_block.check_value = sh_get_uint16be(mem); return zlib_block; } void sh_png_get_bits(sh_png_bit_stream *bits, uint32 bits_required) { //this is an extremely stupid way to make sure the unsigned integer doesn't underflow, this is just a replacement for abs() but on unsigned integers. uint32 extra_bits_needed = (bits->bits_remaining > bits_required) ? (bits->bits_remaining - bits_required) : (bits_required - bits->bits_remaining); uint32 bytes_to_read = extra_bits_needed/8; //because the above is integer division, there is a possiblity of bits to be remaining, i.e: imagine extra_bits_needed is 14, if you do integer division by 8, you get 1, but an extra 6 bits remain if(extra_bits_needed%8) { //do we have any remaining bits? bytes_to_read++; //if we do have extra bits they won't be more than 8 bits, so we will add one extra byte for those bits and we are good to go } for(uint32 i = 0; i < bytes_to_read; ++i) { uint32 byte = *bits->data_stream++; bits->bit_buffer |= byte << (i*8 + bits->bits_remaining); //we need to becareful to not overwrite the remaining bits if any } bits->bits_remaining += bytes_to_read*8; } uint32 sh_png_read_bits(sh_png_bit_stream *bits, uint32 bits_to_read) { uint32 result = 0; if(bits_to_read > bits->bits_remaining) { sh_png_get_bits(bits, bits_to_read); } for(uint32 i = 0; i < bits_to_read; ++i) { uint32 bit = bits->bit_buffer & (1 << i); result |= bit; } bits->bit_buffer >>= bits_to_read; bits->bits_remaining -= bits_to_read; return result; } uint32 sh_peak_bits_reverse(sh_png_bit_stream *bits, uint32 bits_to_peak) { if(bits_to_peak > bits->bits_remaining) { sh_png_get_bits(bits, bits_to_peak); } uint32 result = 0; //this could potentially cause problems, for(uint32 i = 0; i < bits_to_peak; ++i) { result <<= 1; uint32 bit = bits->bit_buffer & (1 << i); result |= (bit > 0) ? 1 : 0; } return result; } int32 sh_png_paeth_predict(int32 a, int32 b, int32 c) { int32 p = a + b - c; int32 pa = sh_abs(p - a); int32 pb = sh_abs(p - b); int32 pc = sh_abs(p - c); if(pa <= pb && pa <= pc) return a; if(pb <= pc) return b; return c; } uint32 sh_decode_huffman(sh_png_bit_stream *bits, uint32 *assigned_codes, uint8 *code_bit_lengths, uint32 assigned_code_length) { for(uint32 i = 0; i < assigned_code_length; ++i) { if(code_bit_lengths[i] == 0) continue; uint32 code = sh_peak_bits_reverse(bits, code_bit_lengths[i]); if(assigned_codes[i] == code) { bits->bit_buffer >>= code_bit_lengths[i]; bits->bits_remaining -= code_bit_lengths[i]; return i; } } return 0; } uint8 sh_get_maximum_bit_length(uint8 *code_bit_lengths, uint32 len_of_array) { uint8 max_bit_length = 0; for(uint32 i = 0; i < len_of_array; ++i) { if(max_bit_length < code_bit_lengths[i]) { max_bit_length = code_bit_lengths[i]; } } return max_bit_length; } void sh_get_bit_length_count(uint32 *code_count, uint8 *code_bit_length, uint32 bit_len_array_len) { for(uint32 i = 0; i < bit_len_array_len; ++i) { code_count[code_bit_length[i]]++; } } void sh_first_code_for_bitlen(uint32 *first_codes, uint32 *code_count, uint32 max_bit_length) { uint32 code = 0; for(uint32 i = 1; i <= max_bit_length; ++i) { code = ( code + code_count[i-1]) << 1; if(code_count[i] > 0) { first_codes[i] = code; } } } void sh_assign_huffman_code(uint32 *assigned_codes, uint32 *first_codes, uint8 *code_bit_lengths, uint32 len_assign_code) { for(uint32 i = 0; i < len_assign_code; ++i) { if(code_bit_lengths[i]) { assigned_codes[i] = first_codes[code_bit_lengths[i]]++; } } } uint32* sh_build_huffman_code(uint8 *code_bit_lengths, uint32 len_code_bit_lengths) { uint32 max_bit_length = sh_get_maximum_bit_length(code_bit_lengths, len_code_bit_lengths); uint32 *code_counts = (uint32 *)sh_memalloc(sizeof(uint32)*( max_bit_length + 1 )); uint32 *first_codes = (uint32 *)sh_memalloc(sizeof(uint32)*(max_bit_length + 1)); uint32 *assigned_codes = (uint32 *)sh_memalloc(sizeof(uint32)*(len_code_bit_lengths));//we have to assign code to every element in the alphabet, even if we have to assign zero sh_get_bit_length_count(code_counts, code_bit_lengths, len_code_bit_lengths); code_counts[0] = 0; //in the real world, when a code of the alphabet has zero bit length, it means it doesn't occur in the data thus we have to reset the count for the zero bit length codes to 0. sh_first_code_for_bitlen(first_codes, code_counts, max_bit_length); sh_assign_huffman_code(assigned_codes, first_codes, code_bit_lengths, len_code_bit_lengths); return assigned_codes; } uint8* sh_zlib_deflate_block( sh_png_bit_stream *bits, uint32 *literal_tree, uint8 *lit_code_bit_len, uint32 lit_arr_len, uint32 *distance_tree, uint8 *dist_tree_bit_len, uint32 dist_arr_len, uint32 *bytes_read) { //1 MB data for the uncompressed block, you can pre allocte a giant memory // that you can pass in, the size of the memory would probaly be something like // bytes_per_pixel * width * height + height*filter_byte //each row has a filter byte(s) in the beginning that you have to account for //when you decompress uint8 *decompressed_data = sh_memalloc(1024*1024); uint32 data_index = 0; while(true) { uint32 decoded_value = sh_decode_huffman(bits, literal_tree, lit_code_bit_len, lit_arr_len); if(decoded_value == 256) break; if(decoded_value < 256) { //its a literal so just output it decompressed_data[data_index++] = decoded_value; continue; } if(decoded_value < 286 && decoded_value > 256) { uint32 base_index = decoded_value - 257; uint32 duplicate_length = base_lengths[base_index] + sh_png_read_bits(bits, base_length_extra_bit[base_index]);; uint32 distance_index = sh_decode_huffman(bits, distance_tree, dist_tree_bit_len, dist_arr_len); uint32 distance_length = dist_bases[distance_index] + sh_png_read_bits(bits, dist_extra_bits[distance_index]); uint32 back_pointer_index = data_index - distance_length; while(duplicate_length--) { decompressed_data[data_index++] = decompressed_data[back_pointer_index++]; } } } *bytes_read = data_index; uint8 *fit_image = sh_memalloc(data_index); sh_memcpy(decompressed_data, fit_image, data_index); sh_memfree(decompressed_data); return fit_image; } uint8* sh_zlib_decompress(uint8 *zlib_data, uint32 *decompressed_size) { uint8 *decompressed_data = sh_memalloc(1024*1024*4); //4 MB free space uint32 data_read = 0; uint32 final; uint32 type; sh_png_bit_stream bit_stream = {zlib_data, 0, 0}; sh_png_bit_stream *bits = &bit_stream; do { final = sh_png_read_bits(bits, 1); type = sh_png_read_bits(bits, 2); uint32 hlit = sh_png_read_bits(bits, 5) + 257; uint32 hdist = sh_png_read_bits(bits, 5) + 1; uint32 hclen = sh_png_read_bits(bits, 4) + 4; uint8 code_lengths_of_code_length_order[] = {16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15}; uint8 code_length_of_code_length[19]; //maximum alphabet symbol is 18 sh_memset(code_length_of_code_length, 0, 19); for(uint8 i = 0; i < hclen; ++i) { code_length_of_code_length[code_lengths_of_code_length_order[i]] = sh_png_read_bits(bits, 3); } uint32 *huffman_codes_of_tree_of_trees = sh_build_huffman_code(code_length_of_code_length, 19); uint8 *two_trees_code_bit_lengths = sh_memalloc(hlit + hdist); //because we have repetition, we won't necessarly have the exact bit lengths for each symbol if we just loop one increment at a time uint32 code_index = 0; while(code_index < (hdist+hlit)) { uint32 decoded_value = sh_decode_huffman(bits, huffman_codes_of_tree_of_trees, code_length_of_code_length, 19); if(decoded_value < 16) { two_trees_code_bit_lengths[code_index++] = decoded_value; continue; } uint32 repeat_count = 0; uint8 code_length_to_repeat = 0; switch(decoded_value) { case 16: repeat_count = sh_png_read_bits(bits, 2) + 3;// 3 - 6 repeat count code_length_to_repeat = two_trees_code_bit_lengths[code_index - 1]; break; case 17: repeat_count = sh_png_read_bits(bits, 3) + 3;// 3 - 10 repeat count break; case 18: repeat_count = sh_png_read_bits(bits, 7) + 11;// 3 - 10 repeat count break; } sh_memset(two_trees_code_bit_lengths + code_index, code_length_to_repeat, repeat_count); code_index += repeat_count; } uint32 *literal_length_huff_tree = sh_build_huffman_code(two_trees_code_bit_lengths, hlit); uint32 *distance_huff_tree = sh_build_huffman_code(two_trees_code_bit_lengths + hlit, hdist); uint32 block_size = 0; uint8 *decompressed_block = sh_zlib_deflate_block( bits, literal_length_huff_tree, two_trees_code_bit_lengths, hlit, distance_huff_tree, two_trees_code_bit_lengths + hlit, hdist, &block_size); sh_memcpy(decompressed_block, decompressed_data + data_read, block_size); data_read += block_size; sh_memfree(decompressed_block); } while(!final); *decompressed_size = data_read; return decompressed_data; } uint8* sh_png_defilter(uint8 *decompressed_image, uint32 size, sh_png_chunk *ihdr) { uint32 x = sh_get_uint32be(ihdr->data); uint32 y = sh_get_uint32be(ihdr->data+4); uint8 bit_depth = *( ihdr->data + 4 + 4 );//count the bytes out uint8 byte_per_pixel = 1;//this is usually determined by checking color type, the picture I'm using is only greyscale, its only one byte per pixel uint8 *row = decompressed_image; uint32 stride = x*byte_per_pixel; uint8 *image = sh_memalloc(x*y*byte_per_pixel); //this is even smaller than the filter but just being safe uint8 *working = image; for(uint32 i = 0; i < y; ++i) { working = image + i*stride; uint8 filter = *row++; switch(filter) { case sh_no_filter: { for(uint32 j = 0; j < x; ++j) { working[j] = row[j]; } } break; case sh_sub_filter: { for(uint32 j = 0; j < x; ++j) { uint8 a = 0; if(j != 0) { a = working[j-1]; } uint8 value = row[j] + a; working[j] = value; } } break; case sh_up_filter: { uint8 *prev_row = working - stride; for(uint32 j = 0; j < x; ++j) { uint8 b = prev_row[j]; uint8 value = row[j] + b; working[j] = value; } } break; case sh_avg_filter: { uint8 *prev_row = working - stride; for(uint32 j = 0; j < x; ++j) { uint8 a = 0; uint8 b = prev_row[j]; if(j) { a = working[j - 1]; } uint8 value = row[j] + ( (a + b) >> 1 ); working[j] = value; } } break; case sh_paeth_filter: { uint8 *prev_row = working - stride; for(uint32 j = 0; j < x; ++j) { uint8 a = 0; uint8 b = prev_row[j]; uint8 c = 0; if(j) { a = working[j - 1]; c = prev_row[j - 1]; } uint8 value = row[j] + sh_png_paeth_predict((int32) a, (int32) b, (int32) c); working[j] = value; } } break; } row += stride; } return image; } int main(int argc, char **argv) { uint8 *mem = sh_read_file("sh_font_0.png"); SKIP_BYTES(mem, 8); //skip signature, you can read it and check for stuff sh_png_chunk chunks[3]; uint8 *for_reading = mem; //we don't want to lose the pointer of the file for(uint8 i = 0; i < 3; ++i) { chunks[i] = sh_png_read_chunk(for_reading); SKIP_BYTES(for_reading, 4 + 4 + chunks[i].data_length + 4); //Length bytes, type, actual data of the chunk, crc value } //First chunk is IHDR, 2nd is one IDATA chunk, last one is IEND sh_zlib_block zlib_block = sh_read_zlib_block(chunks[1].data, chunks[1].data_length); uint32 decompressed_data_size = 0; uint8 *decompressed_png = sh_zlib_decompress(zlib_block.data, &decompressed_data_size); uint8 *image = sh_png_defilter(decompressed_png, decompressed_data_size, &chunks[0]); return 0; } |
I forgot to include a resource that helped me understand the gzip format:
http://commandlinefanatic.com/cgi-bin/showarticle.cgi?article=art001
Edited by Ben Visness
on
Reason: fixed up bbcode to be compliant with new parser
Good stuff! Huge +1 for writing this down.
Gosh, yeah! I haven't read it yet, but trust Mārtiņš that this is one hell of a first post to a forum. ++Sharlock93;
Thanks for the post.
Some feedback:
- The first paragraph is one long sentence with 2 "because" which make it a bit hard to read.
- You missed a [ / b ] somewhere so the text is in bold for some time
- When you explain the zlib block, the code for sh_read_zlib_block as the parameter name length_of_data instead of length
- SKIP_BYTES doesn't force the mem parameter to a byte size, so if you pass a pointer to a uint32 it would skip 4 time the number of bytes.
Some feedback:
- The first paragraph is one long sentence with 2 "because" which make it a bit hard to read.
- You missed a [ / b ] somewhere so the text is in bold for some time
- When you explain the zlib block, the code for sh_read_zlib_block as the parameter name length_of_data instead of length
- SKIP_BYTES doesn't force the mem parameter to a byte size, so if you pass a pointer to a uint32 it would skip 4 time the number of bytes.
Edited by Simon Anciaux
on
mrmixer
Thanks for the post.
Some feedback:
- The first paragraph is one long sentence with 2 "because" which make it a bit hard to read.
- You missed a [ / b ] somewhere so the text is in bold for some time
- When you explain the zlib block, the code for sh_read_zlib_block as the parameter name length_of_data instead of length
- SKIP_BYTES doesn't force the mem parameter to a byte size, so if you pass a pointer to a uint32 it would skip 4 time the number of bytes.
thanks for the feedback, fixed them:
- first paragraph has a comma now.
- the tags were actually closed and it was on purpose, but yes I did change the closing tags position
- length_of_data is now length, somehow I forgot to copy paste the function signature, as I actually made sure every piece of code ran.
- SKIP_BYTES should only be used on (uint8 *) types, I should have indicated that.
Sharlock93
Implementing a Basic PNG reader the handmade way
English is not my native language, please do give me feedback on both spelling and grammar
A few sentences in, I forgot that you were not a native English speaker. I had to go back and check for grammatical errors, but the only thing that I think is worth mentioning is that sometimes your sentences are too long. This leads you to occasionally comma splice. Don't be afraid to break your sentences up more.
I'm sure other copy-editing remarks could be said, but what's most important for you to know is this: you have excellent English and more importantly, excellent communication skills.
Oswald_HurlemSharlock93
Implementing a Basic PNG reader the handmade way
English is not my native language, please do give me feedback on both spelling and grammar
A few sentences in, I forgot that you were not a native English speaker. I had to go back and check for grammatical errors, but the only thing that I think is worth mentioning is that sometimes your sentences are too long. This leads you to occasionally comma splice. Don't be afraid to break your sentences up more.
I'm sure other copy-editing remarks could be said, but what's most important for you to know is this: you have excellent English and more importantly, excellent communication skills.
Thanks, I have been around the english language for 10+ years, mainly because I was in a private school and english was used as the main language, unfortunately I have zero knowledge about the grammar, when I speak I know if something makes sense but on paper, zero clue, Any idea what a good resource might be for learning the English grammar in a better way?
Many thanks for sharing
Sharlock93
Thanks, I have been around the english language for 10+ years, mainly because I was in a private school and english was used as the main language, unfortunately I have zero knowledge about the grammar, when I speak I know if something makes sense but on paper, zero clue, Any idea what a good resource might be for learning the English grammar in a better way?
This is perfect for you.
https://www.amazon.com/Sense-Styl...ing-Persons-Writing/dp/0143127799
It's a recent book that serves the same purpose as Strunk & White, but gives more modern rules which are grounded in contemporary linguistics and cognitive science. It's by one of the best science authors. He knows what he's talking about.
Edited by Oswald Hurlem
on
Oswald_HurlemSharlock93
Thanks, I have been around the english language for 10+ years, mainly because I was in a private school and english was used as the main language, unfortunately I have zero knowledge about the grammar, when I speak I know if something makes sense but on paper, zero clue, Any idea what a good resource might be for learning the English grammar in a better way?
This is perfect for you.
https://www.amazon.com/Sense-Styl...ing-Persons-Writing/dp/0143127799
It's a recent book that serves the same purpose as Strunk & White, but gives more modern rules which are grounded in contemporary linguistics and cognitive science. It's by one of the best science authors. He knows what he's talking about.
Perfect.